Implizite Volatilität – Definition & Berechnung

Die implizite Volatilität (IV), engl.: „Implied Volatility“, ist eine Optionskennzahl, die ein Maß für die aktuell am Markt erwartete Schwankungsbreite des Basiswertes über die Restlaufzeit der Option darstellt. Sie ist eine der wichtigsten Kennzahlen im Optionshandel und spielt bei der Auswahl der richtigen Optionsstrategie eine entscheidende Rolle.

Implizite Volatilität – Definition und Erklärung

Die implizite Volatilität ist ein aus den aktuellen Optionspreisen abgeleiteter Wert. Sie stellt die am Markt eingepreisten Erwartungen bezüglich der künftigen Schwankungsbreite der Wertpapierrenditen des Basiswerts (Underlying) während der Laufzeit der Option dar.

Folgende Kernaussagen können allgemein getroffen werden:

• Grundsätzlich drückt ein hoher Wert der impliziten Volatilität eine höhere erwartete Schwankungsbreite aus als ein niedriger
• Die implizite Volatilität nimmt zu, wenn die Marktschwankungen zunehmen, sprich die Unsicherheit an den Märkten zunimmt oder wirtschaftlich relevante Events, wie Zinsentscheide und Unternehmenszahlen anstehen
• Stark verallgemeinert kann man sagen: Bei ansonsten gleichen Parametern sind Optionen mit einer geringen impliziten Volatilität preiswerter als Optionen mit einer hohen impliziten Volatilität (weiterführende Artikel: Implied Volatility Rank (IV Rank) und IV Percentile vs. IV Rank)
• Nimmt die implizite Volatilität rasant ab, nachdem sie sich zunächst aufgebaut hatte, ist von einem Implied Volatility Crush (IV Crush) die Rede
• Die Kennzahl drückt die Breite der Schwankung und nicht deren Richtung aus

Historische Volatilität vs. implizite Volatilität

Generell können zwei Arten von Volatilitäten unterschieden werden: historische und implizite Volatilität.

• Die historische Volatilität berücksichtigt ausschließlich vergangenheitsbezogene Daten eines Wertpapiers. Entsprechend bildet sie die vergangene Schwankungsintensität der Wertpapierrenditen in einem entsprechenden Zeitintervall ab.
• Die implizite Volatilität spiegelt hingegen die zukünftig erwartete Schwankung der Wertpapierrenditen wider und kann in ihrer Höhe signifikant von der historischen Volatilität abweichen. Die in Optionen und Optionsscheinen abgebildete Volatilität entspricht genau dieser impliziten Volatilität.

Berechnung der impliziten Volatilität

Die implizite Volatilität wird mit Hilfe eines Iterationsverfahrens und eines finanzmathematischen Optionspreismodells (z. B. Black-Scholes-Merton-Modell) abgeleitet. Der Grund dafür ist, dass die Volatilität implizit in der Formel enthalten ist und nicht direkt berechnet werden kann. Wie die historische Volatilität ist auch dieses Ergebnis annualisiert.

Der Optionsgrieche Vega

Der Einfluss der impliziten Volatilität auf den Optionspreis wird mit dem Optionsgriechen Vega angegeben. Das Vega entspricht der ersten partiellen Ableitung des Optionspreises nach der Volatilität. Die Kennzahl gibt an, wie sich der Preis der Option in Relation zu einer sich veränderten Volatilität ändert.

Folglich misst das Vega, wie hoch die Änderung des Optionspreises ausfällt, wenn sich die implizite Volatilität um einen Prozentpunkt ändert. Beim Vega handelt es sich somit um eine direkte Sensitivität des Werttreibers Volatilität. Die Volatilität wird in Optionspreismodellen häufig durch das Symbol σ (Sigma) gekennzeichnet.

VIX als Indikator für die implizite Volatilität

Die implizite Volatilität wird von verschiedenen Indizes abgebildet. Der bekannteste Volatilitätsindex ist der CBOE Volatility Index (VIX). Der VIX spiegelt die Markterwartungen hinsichtlich der erwarteten Volatilität wider. Die Berechnung erfolgt anhand der Echtzeitpreise von Optionen auf den S&P 500 Index (Symbol: SPX).

Da der VIX Index die implizite Volatilität misst, sind die Indexwerte wie folgt zu deuten:

• Ein hoher Indexstand geht mit einer volatilen und unruhigen Marktphase einher, während niedrige Indexwerte eine Kursentwicklung des S&P 500 ohne starke Kursschwankungen erwarten lassen.
• Entsprechend besteht zwischen dem VIX Index und dem S&P 500 eine negative Korrelation. Fällt der Kurs des S&P 500, dann steigt in der Regel der VIX Index an. Hingegen fällt der VIX Index, wenn der Kurs des S&P 500 steigt.

Diese Beziehung ist jedoch nicht perfekt und sollte mit Vorsicht interpretiert werden, da der VIX keinen Aufschluss über die Richtung der zu erwartenden Kursschwankungen gibt.

Optionsstrategie für steigende implizite Volatilität

Beim sog. Long Straddle handelt es sich um eine neutrale Handelsstrategie, um von einem Anstieg der impliziten Volatilität zu profitieren. Grundsätzlich geht ein Anleger hier davon aus, dass die Volatilität des Underlyings in einem bestimmten Zeitraum ansteigen wird. Hierzu erwirbt er gleichzeitig eine Put-Option und eine Call-Option auf dasselbe Underlying, wobei sowohl der Strike-Preis als auch die Fälligkeit bei beiden Optionen identisch sind.

Durch die gleichzeitige Long-Position, sowohl im Put als auch im Call, profitiert diese Strategie sowohl von signifikanten Kursbewegungen als auch vom Anstieg der impliziten Volatilität in den beiden Optionen. Eine steigende implizite Volatilität erhöht den sog. Zeitwert der Option und gleichzeitig den Optionspreis, der sich aus der Summe von Zeitwert und innerer Wert der Option ergibt.

Optionsstrategie für sinkende implizite Volatilität

Ähnlich wie beim Long Straddle handelt es sich beim Short Strangle um eine neutrale Handelsstrategie, die allerdings ausschließlich mit Optionen umgesetzt werden kann (nicht mit Optionsscheinen).

Grundsätzlich geht ein Anleger bei dieser Strategie davon aus, dass der Kurs des Underlyings in einem bestimmten Zeitraum innerhalb einer gewissen Range oszilliert. Hierzu verkauft er gleichzeitig einen Put und einen Call auf dasselbe Underlying (in der Fachsprache spricht man auch davon, dass der Stillhalter eine Option schreibt), wobei die Strikes voneinander abweichen, die Fälligkeit beider Optionen jedoch identisch ist.

Durch die gleichzeitige Short-Position, sowohl im Put als auch im Call, profitiert diese Strategie profitiert sowohl von sich kaum bewegenden Kursen als auch von der Abnahme der impliziten Volatilität in beiden Optionen. Eine sinkende implizite Volatilität verringert den sog. Zeitwert der Option und gleichzeitig den Optionspreis, der sich wie erwähnt aus der Summe von Zeitwert und innerer Wert der Option ergibt.

Implizite Volatilität über verschiedene Strikes und Laufzeiten

Entgegen einer häufigen Vereinfachung gibt es am Markt nicht nur eine einzige implizite Volatilität für einen Underlying. Grundsätzlich besitzt jede einzelne Option ihre eigene implizite Volatilität.

In der Praxis bedeutet das:

• Zwei Optionen auf denselben Basiswert können trotz identischer Fälligkeit unterschiedliche implizite Volatilitäten aufweisen, wenn sich ihre Strike-Preise unterscheiden.
• Umgekehrt können auch Optionen mit gleichem Strike voneinander abweichende implizite Volatilitäten besitzen, wenn ihre Restlaufzeiten unterschiedlich sind.

Volatility Smile / Skew / Surface bzw. Laufzeitstruktur

Die Verteilung der impliziten Volatilität über verschiedene Strikes und Laufzeiten folgt in der Praxis nur selten einem einheitlichen Muster. Häufig zeigen sich wiederkehrende Strukturverläufe, die im Optionshandel unter Begriffen wie Volatility Smile, Volatility Skew und Volatility Surface zusammengefasst werden.

Volatility Smile

Von einem Volatility Smile ist die Rede, wenn Optionen gleicher Restlaufzeit im Bereich At The Money (ATM) eine geringere implizite Volatilität aufweisen als Optionen, die deutlich In The Money (ITM) oder Out of The Money (OTM) notieren. Trägt man die implizite Volatilität über die verschiedenen Strikes hinweg ab, erinnert die Kurve an ein Lächeln.

Volatility Skew

Von einem Volatility Skew spricht man, wenn die implizite Volatilität bei gegebener Laufzeit mit dem Strike systematisch zu- oder abnimmt. Besonders an Aktien- und Aktienindexmärkten ist häufig zu beobachten, dass weit aus dem Geld liegende Put-Optionen eine höhere implizite Volatilität besitzen als vergleichbare Call-Optionen. Der Grund liegt unter anderem in der erhöhten Nachfrage nach Absicherungen gegen fallende Kurse.

Volatility Surface und Laufzeitstruktur

Werden nicht nur verschiedene Strikes, sondern gleichzeitig auch unterschiedliche Restlaufzeiten betrachtet, ergibt sich die sog. Volatility Surface bzw. Volatilitätsoberfläche. Sie zeigt, wie sich die implizite Volatilität gleichzeitig in Abhängigkeit vom Strike und von der Laufzeit verändert.

Die auf die Restlaufzeit bezogene Struktur wird häufig auch als Laufzeitstruktur oder Term Structure der impliziten Volatilität bezeichnet. In ruhigen Marktphasen können länger laufende Optionen eine höhere implizite Volatilität aufweisen als kurzfristige. Vor wichtigen Ereignissen, wie Unternehmenszahlen oder Notenbanksitzungen, ist hingegen oft zu beobachten, dass die implizite Volatilität kurzer Laufzeiten überproportional ansteigt.

Weiterführende Informationen

Exkurs: Volatilität | Standardabweichung

Die Volatilität ist in der Finanzökonomie die meistbeachtete Kennzahl, wenn es um die Bestimmung des Risikos geht. Üblicherweise wird die Volatilität mithilfe der statistischen Kennzahl Standardabweichung gemessen, die sich im Rahmen des Optionshandels typischerweise als annualisierte Standardabweichung von Preisänderungen bzw. Renditen ausdrücken lässt.

In der Literatur werden Risiko, Volatilität und Standardabweichung oft als Synonym verwendet. Teilweise wird auch von der sog. Varianz gesprochen, die sich aus dem Quadrat der Standardabweichung ergibt.

Allerdings ist die Varianz für finanzmathematische Untersuchungen von Privatanlegern eher ungeeignet, da sie nicht intuitiv verständlich ist. Deswegen findet überwiegend die Standardabweichung bei der Risikoermittlung Anwendung, da sie in der gleichen Einheit wie die zugrundeliegende Rendite angegeben wird.

Standardabweichung als Risikomaß

Auf die Börse bezogen, ist die Standardabweichung eine statistische Kennzahl für die Streuung der Wertpapierrenditen im Zeitablauf um ihren arithmetischen Mittelwert herum. Erst durch die Ermittlung dieser Kennzahl lassen sich Aussagen über das Risiko treffen.

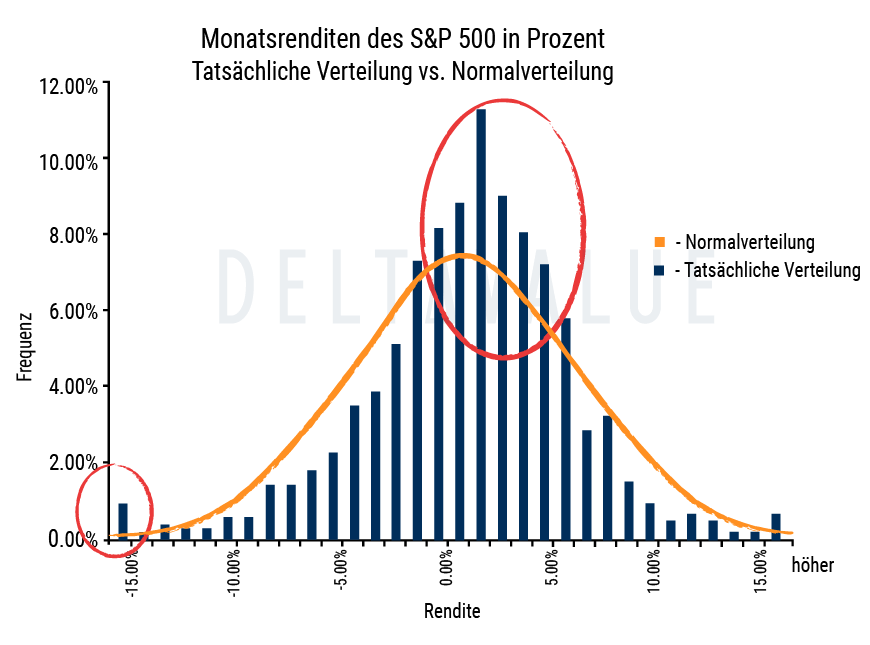
Die Standardabweichung ist also ein Streuungsmaß, dem die sog. Normalverteilung zugrunde liegt. Dabei gilt es zu beachten, dass Wertpapierrenditen nur näherungsweise normalverteilt sind. Je länger der Betrachtungszeitraum, umso weniger weichen die Renditen von einer Normalverteilung ab.

Die Volatilität entspricht also der Standardabweichung, die als Quadratwurzel der durchschnittlichen quadratischen Abweichung der Wertpapierrenditen von ihrem Mittelwert definiert ist.

Anders formuliert: Die Summe der quadrierten Abweichungen aller Renditen vom arithmetischen Mittel, wird durch die Anzahl der Renditen dividiert und daraus wird die Quadratwurzel gezogen. Noch einfacher formuliert, aber auch verallgemeinert könnte man sagen, die Standardabweichung ist ein Streuungsmaß um den Durchschnitt.

Bedeutung der Normalverteilung

Da die korrekte Interpretation der Standardabweichung einen hohen Stellenwert im Optionshandel einnimmt, sei an dieser Stelle ein kurzer Exkurs über die wichtigsten Merkmale der Normalverteilung gestattet:

• Eine Standardabweichung: 68,27 % aller Messwerte liegen maximal eine Standardabweichung vom Durchschnitt entfernt. Dabei liegt die Hälfte der Werte, also 34,135 %, maximal eine Standardabweichung unter dem Durchschnitt, während die andere Hälfte maximal eine Standardabweichung über dem Durchschnitt liegt.
• Zwei Standardabweichungen: 95,45 % aller Messwerte liegen maximal zwei Standardabweichungen vom Durchschnitt entfernt. Dabei liegt die Hälfte der Werte, also 47,725 %, maximal zwei Standardabweichungen unter dem Durchschnitt, während die andere Hälfte maximal zwei Standardabweichungen über dem Durchschnitt liegt.
• Drei Standardabweichungen: 99,73 % aller Messwerte liegen maximal drei Standardabweichungen vom Durchschnitt entfernt. Dabei liegt die Hälfte der Werte, also 49,865 %, maximal drei Standardabweichungen unter dem Durchschnitt, während die andere Hälfte maximal drei Standardabweichungen über dem Durchschnitt liegt.

Demzufolge liegen 31,73 % aller Werte mehr als eine Standardabweichung vom Durchschnitt entfernt. Dabei gilt wieder, dass jeweils die Hälfte von 31,73 %, also 15,865 %, über bzw. unter dem Durchschnitt liegt. Das bedeutet, dass etwas mehr als jeder sechste Wert schlechter bzw. besser als der Durchschnitt abzüglich bzw. zuzüglich einer Standardabweichung sein wird.