Volatilität an der Börse – Definition & Berechnung
Volatilität (englisch: „volatility“) ist ein Maß für die Schwankungsbreite des Kurses eines Wertpapiers oder eines Marktindexes relativ zu seinem Durchschnittskurs in einem bestimmten Zeitraum. Je höher die Volatilität, desto stärker weicht beispielsweise der Kurs einer Aktie von ihrem Durchschnittskurs ab.
Während die historische Volatilität die in der Vergangenheit beobachteten Kursschwankungen analysiert, prognostiziert die implizite Volatilität die erwartete Intensität zukünftiger Kursschwankungen, die häufig aus Optionspreisen abgeleitet wird – und zwar unabhängig des Trends.
🔴 Live-Webinar am 29.04.2024 um 18:30 Uhr
Ausbildung für Vermögensaufbau mit zusätzlichen monatlichen Einnahmen
Generiere ein zusätzliches regelmäßiges Einkommen an der Börse, indem du ein klares Handelssystem mit sofort umsetzbarem Investment-Wissen erlernst. Lerne Strategien kennen, die dir einen statistisch und wissenschaftlich belegbaren Vorteil an der Börse verschaffen.
 Gute von schlechten Aktien unterscheiden
Gute von schlechten Aktien unterscheiden
Profitable Aktien- und Optionsstrategien
In jeder Marktlage Geld verdienen
Plus Gratis-PDF im Webinar: Dein Start in den erfolgreichen Optionshandel
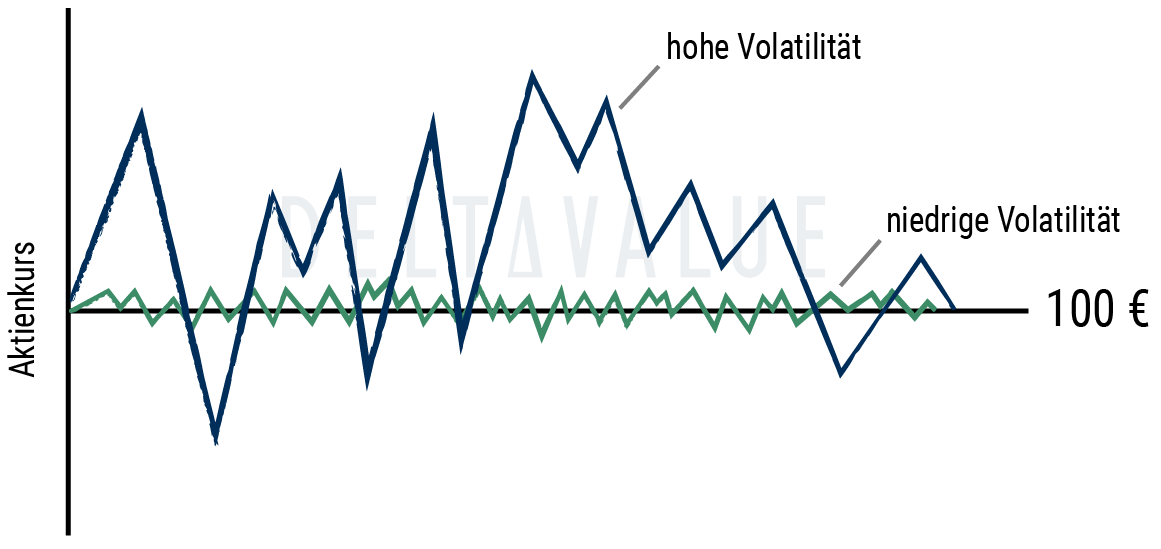
Volatilität – Definition
Volatilität beschreibt die Schwankungsbreite z.B. eines Aktienkurses um einen Mittelwert. Eine hohe Aktienvolatilität bedeutet, dass der Aktienkurs stark und oft unvorhersehbar schwankt, was auf ein höheres Anlagerisiko hinweist.
Investitionen in Aktien mit hoher Volatilität können potenziell höhere Gewinne, aber auch höhere Verluste mit sich bringen. Bei niedriger Volatilität liegen die einzelnen Datenpunkte näher beieinander, was als geringeres Anlagerisiko interpretiert werden kann.
Wie kommt es zu Volatilität?
Ein volatiler Markt ist durch schnelle und starke Preisänderungen gekennzeichnet. Diese können durch verschiedene Faktoren verursacht werden, wie z.B. Wirtschaftsnachrichten, politische Ereignisse, unternehmensspezifische Ereignisse, globale Entwicklungen oder andere marktrelevante Gründe, wie z.B. Spekulationen und Gerüchte und Liquiditätsengpässe.
Insbesondere Wirtschaftsdaten wie
- Arbeitsmarktberichte,
- Inflationsraten,
- Zinsentscheidungen von Zentralbanken und
- BIP-Wachstumszahlen können die Märkte erheblich beeinflussen.
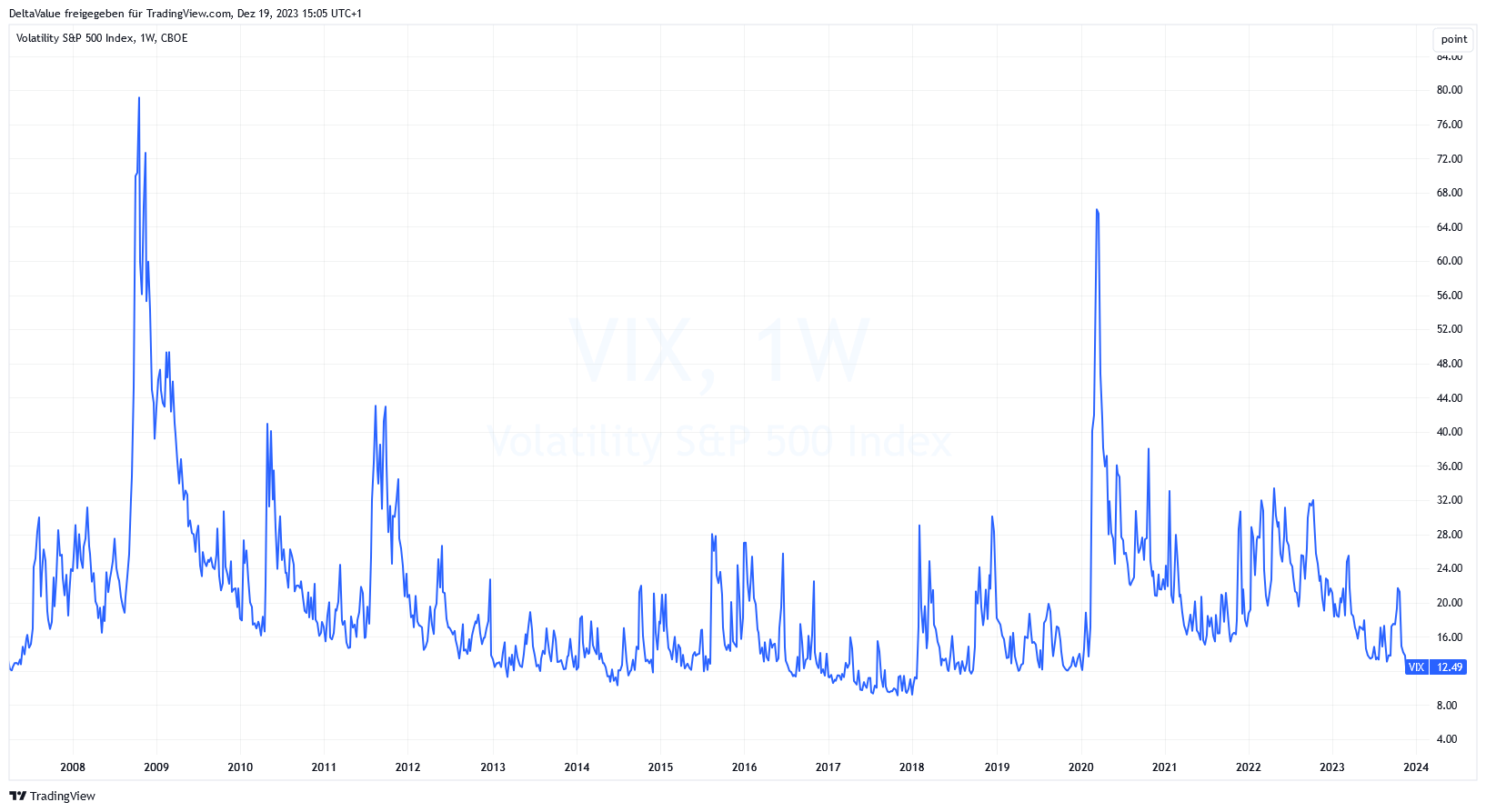
Volatilitätsindex (VIX)
Es gibt spezielle Indizes, wie den CBOE Volatility Index (VIX), der die erwartete Volatilität des S&P 500 innerhalb der nächsten ca. 30 Tage misst. Solche Indizes werden oft als „Angstbarometer“ des Marktes angesehen.
Der VIX wird auf Basis von auf den S&P 500 lautende Indexoptionen berechnet. In ruhigen Marktphasen ist er tendenziell gering, in unruhigen Marktphasen tendenziell hoch.
Historisch gesehen deutet ein VIX-Wert von über 20 auf ein volatileres Börsenumfeld hin, in dem die Unsicherheit unter den Marktteilnehmern relativ hoch ist, auch wenn diese Unsicherheit nicht immer gerechtfertigt sein muss. Werte unter 15 deuten hingegen auf ruhigere Marktphasen hin, in denen sich die Kurse in der Regel stabiler entwickeln.
Bedeutung für den Optionshandel
Sowohl bei Wertpapieranlagen im Allgemeinen als auch beim Optionshandel im Besonderen spielt Volatilität eine wesentliche Rolle. Bei Optionen steigt mit zunehmender Volatilität die zu zahlende Prämie. Der Grund dafür ist, dass bei höheren tatsächlichen, d.h. historischen Volatilitäten die Marktteilnehmer einen höheren Absicherungsbedarf haben, so dass die Nachfrage nach Optionen generell steigt.
Gleichzeitig ist die Wahrscheinlichkeit – unter Konstanthaltung aller anderen Einflussfaktoren (ceteris paribus) – höher, dass die Option am Ende im Geld (in the money) fällig wird. Für diese höhere Wahrscheinlichkeit wird der Verkäufer der Option tendenziell auch eine höhere Prämie verlangen.
Die dann höhere Prämie kann ein Hinweis auf die zukünftig erwartete Schwankungsintensität der Kurse sein, die Höhe der Prämie impliziert also gewissermaßen die erwartete Volatilität.
Die Unterscheidung zwischen historischer und impliziter Volatilität ist daher wichtig und kritisch. Für die allermeisten Basiswerte bzw. Wertpapiere (z.B. Aktien, Unternehmensanleihen, Rohstoffe etc.) ist die historische Rendite von Interesse. Insbesondere bei Optionen spielt hingegen auch die implizite Volatilität eine zentrale Rolle.
Berechnung der Volatilität
Die Formel zur Ermittlung der Volatilität ist die Wurzel der gewichteten, quadrierten Abweichungen der einzelnen Merkmale (bspw. der einzelnen Aktienrenditen) um den Mittelwert.
Wird die Wurzel nicht gezogen, erhält man die Varianz. Varianz und Volatilität sind somit zwei eng verwandte Kennzahlen. Tabellenkalkulationsprogramme wie Excel oder Google Sheets bieten spezielle Formeln, mit denen die Volatilität direkt aus einer Zeitreihe herausgerechnet werden kann.
Beispiel – Volatilität bei Aktienrenditen
An diesem Beispiel wird die Berechnung der Volatilität besser ersichtlich. Bezogen auf die Schwankungsbreite von Aktienkursen ist zunächst wichtig, dass nicht die Kurse bzw. Preise selbst herangezogen werden, sondern die Renditen, die den Kursen zugrunde liegen.
Wird beispielsweise die Volatilität einer Aktie bezogen auf die täglichen Veränderungen berechnet, sind zunächst die prozentualen Veränderungen zwischen den jeweiligen Tagen zu berechnen (=Aktienrenditen).
| Kurs Beginn Monat 1 | Kurs Ende Monat 1 | Rendite Monat 1 |
| 62 EUR | 66 EUR | +6,5 % |
| 66 EUR | 74 EUR | +12,1 % |
| 74 EUR | 78 EUR | +5,4 % |
| 78 EUR | 70 EUR | -10,3 % |
Mittelwert
Der Mittelwert lässt sich zunächst leicht ermitteln. Die vorhandenen Renditen werden addiert und durch die Anzahl der Messpunkte geteilt. Hier gibt es vier Monatsrenditen, die für den Mittelwert addiert und durch vier geteilt werden müssen.
Standardabweichung
Mit dem Mittelwert kann jetzt auch die Formel der Volatilität bzw. Standardabweichung vervollständigt werden. Im konkreten Beispiel wird die Volatilität wie folgt berechnet:
Nachteile der Volatilität
Je nach Perspektive sind einige Nachteile in Bezug auf den Volatilitätsbegriff zu berücksichtigen.
- Ein zentraler Nachteil der Volatilität im Kontext des häufig im Kapitalmarkt verwendeten Synonyms „Risiko“ ist die Tatsache, dass es weitere Risikoformen gibt, die nicht lediglich die Schwankung um einen Mittelwert meinen. Beispielsweise ist das Totalverlustrisiko ebenfalls eine verbreitete Risikodefinition, die aber vielmehr nur zwei Zustände kennt: Totalverlust oder kein Totalverlust.
- Risiko im Sinne der Volatilität ist eine Abweichung vom Mittelwert in beide Richtungen. Damit kann das Risiko eine Abweichung nach oben oder nach unten bedeuten. Viele Anleger betrachten steigende Kurse in diesem nicht als Risiko, aber nach dieser Definition wären sie es.
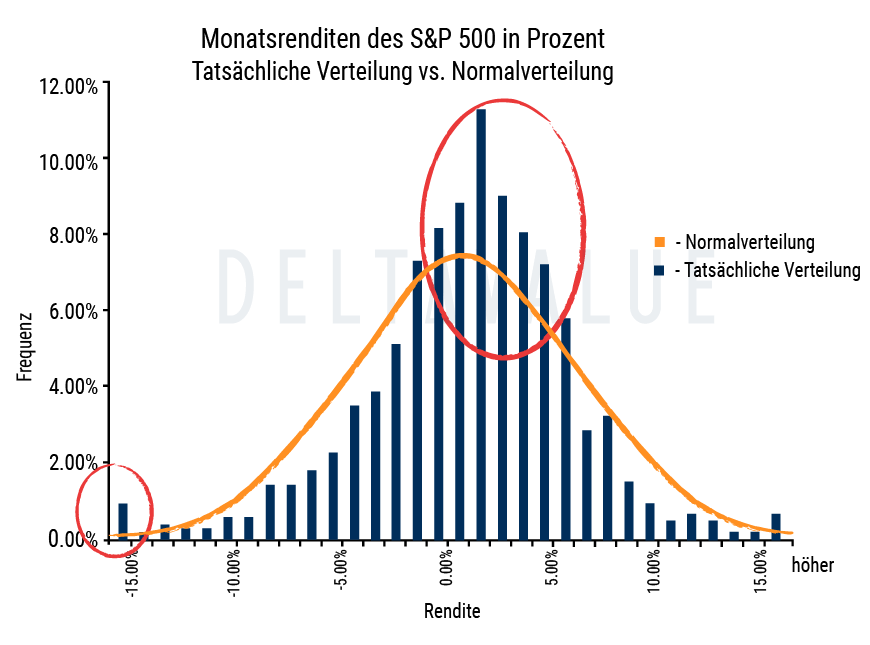
- Bei der Analyse bzw. Prognose von Extremevents, also unerwartet starken Kursausschlägen in beide Richtungen („Black Swans“ bzw. „Schwarze Schwäne“), muss berücksichtigt werden, dass bspw. Aktienpreisrenditen nicht normalverteilt sind. Andere Wahrscheinlichkeitsverteilungen wie die t-Verteilung liefern realitätsnäherer Ergebnisse.
Häufige Fragen
Was ist die historische Volatilität?
Die historische Volatilität (auch "realisierte Volatilität") drückt lediglich die Schwankung der Wertpapiere um einen Mittelwert aus. Die Berechnung wurde bereits weiter oben beschrieben und zeigt, dass es sich um eine vergangenheitsorientierte Sichtweise handelt.
Alle Kursschwankungen eines Wertpapiers, Basiswertes, Indexes etc. werden retrospektiv betrachtet, um die Volatilität zu ermitteln. Die Aussagekraft für die Zukunft ist daher begrenzt. Da sich die Schwankungsbreite von Wertpapierkursen ändern kann, lässt sie sich nur bedingt in die Zukunft fortschreiben.
Was ist die implizite Volatilität?
Im Gegensatz zur historischen Volatilität handelt es sich bei der impliziten Volatilität um eine zukunftsgerichtete Betrachtung. Die implizite Volatilität kann ausschließlich durch die theoretische Preisberechnung bzw. Bewertung von Optionen berechnet werden.
Vereinfacht gesagt, wird der tatsächlich am Markt gehandelte Optionspreis abgelesen und in ein mathematisches Modell zur Berechnung des theoretisch erwarteten Optionspreises (bspw. Black-Scholes-Modell) eingesetzt.
Anschließend wird diese Formel nach der Volatilität aufgelöst. Diese sich ergebende Abweichung ist daher die implizite Volatilität, denn sie drückt aus, wie hoch die Schwankungsintensität sein müsste, gegeben der tatsächlich am Markt gehandelte Optionspreis sei korrekt.
Auf den zweiten Blick wird daher deutlich, dass die implizite Volatilität einen Rückschluss über die Angebot-Nachfrage-Situation einer bestimmten Option hat. Eine hohe Nachfrage nach Optionen lässt deren Preis bzw. Prämie steigen, weswegen implizit davon ausgegangen wird, dass der Markt in der Zukunft eine höhere Schwankungsbreite erwartet.
Offizielle, vorab terminierte Bekanntmachungen und Berichtstermine wie etwa Quartalszahlen sind bei Unternehmen grundsätzlich Auslöser für eine steigende implizite Volatilität.
Egal, ob es eine positive oder negative Erwartung gegenüber dem Berichtstermin gibt, die Marktteilnehmer rechnen mit einer stärkeren Schwankung der Kurse. Ein Anstieg der Absicherungsgeschäfte, also beispielsweise der Kauf von Call-Optionen oder Put-Optionen, treibt die Optionspreise und somit die implizite Volatilität.
Kostenloses Webinar + PDF: So handelst du profitabel mit Optionen und generierst ein Zusatzeinkommen
 Lerne in unserem kostenlosen Live-Webinar am 29.04.2024 um 18:30 Uhr, wie du mit dem Optionshandel ein regelmäßiges Zusatzeinkommen aufbaust. Lerne, gute von schlechten Aktien zu unterscheiden und erkenne zuverlässig überteuerte Aktienkurse. Baue dir ein zweites Einkommen auf, mit dem du unabhängig der Marktlage Geld verdienen kannst. Klicke hier, um dich für das Webinar anzumelden.
Lerne in unserem kostenlosen Live-Webinar am 29.04.2024 um 18:30 Uhr, wie du mit dem Optionshandel ein regelmäßiges Zusatzeinkommen aufbaust. Lerne, gute von schlechten Aktien zu unterscheiden und erkenne zuverlässig überteuerte Aktienkurse. Baue dir ein zweites Einkommen auf, mit dem du unabhängig der Marktlage Geld verdienen kannst. Klicke hier, um dich für das Webinar anzumelden.