Black-Scholes-Modell – Erklärung & Bedeutung

Black-Scholes-Modell – Definition

Das Black-Scholes-Modell ist ein finanzmathematisches Modell, welches den theoretischen Wert von Optionen und anderen Anlageinstrumenten berechnet. Die Ergebnisse sind in der Regel akkurat. Das Modell kann jedoch aufgrund von bestimmten Grundannahmen Werte ermitteln, die von den realen Optionspreisen abweichen.

Bestandteile der Black-Scholes-Gleichung

Die Black-Scholes-Gleichung erfordert fünf Variablen. Diese Inputs sind

• Volatilität,
• Kurs des Basiswertes,
• Strike-Preis der Option,
• die Zeit bis zum Verfall der Option und der risikofreie Zinssatz.

Mithilfe dieser Variablen können Optionsverkäufer (Stillhalter) faire Preise für die von ihnen verkauften Optionen festlegen.

Black-Scholes-Modell – Berechnung

Das Black-Scholes-Modell unterliegt einigen Annahmen, welche notwendig sind, um die Berechnung so genau wie möglich durchführen zu können. Den folgenden Annahmen unterliegt die Berechnung:

• Während der Laufzeit der Option werden keine Dividenden ausgezahlt.
• Marktbewegungen geschehen zufällig, das heißt es können keine Marktbewegungen vorausgesagt werden.
• Es fallen keine Transaktionskosten beim Kauf der Option an.
• Der risikofreie Zinssatz und die Volatilität des Basiswertes sind bekannt und konstant.
• Die Renditen des Basiswertes sind lognormalverteilt.
• Die Option ist europäisch und kann nur bei Fälligkeit ausgeübt werden.

Herleitung der Black-Scholes Formel

Unter Berücksichtigung aller oben genannten Annahmen kann nun für die Bestimmung des fairen Preises (Fair Value) einer Call-Option folgendes Black-Scholes-Modell aufgestellt werden:

Für die Bestimmung des Fair Value einer Put-Option, wird nachfolgendes Black-Scholes-Modell herangezogen:

wobei d1 und d2 wie folgt ermittelt werden:

Erweitert um die Dividendenzahlungen, ergibt sich folgende Formel für eine Call-Option:

Und entsprechend folgende Formel für eine Put-Option:

Unter Zuhilfenahme der Black-Scholes Formel, können die Effekte der identifizierten Werttreiber bzw. Einflussfaktoren Strike K, Kurs des Underlying S_o, Volatilität σ, Restlaufzeit T, risikofreier Zinssatz r_f und Dividende D numerisch aufgezeigt werden.

Black-Scholes-Modell – Bedeutung

Das Black-Scholes-Modell wurde 1973 von Fischer Black, Robert Merton und Myron Scholes entwickelt und war die erste weitverbreitete mathematische Methode zur Berechnung des theoretischen Werts eines Optionskontrakts unter Verwendung der aktuellen Aktienkurse, des Ausübungspreises der Option (Strike Preis), der erwarteten Zinssätze, der Zeit bis zum Ablauf und der erwarteten Volatilität.

Die ursprüngliche Gleichung wurde in dem 1973 im Journal of Political Economy veröffentlichten Aufsatz „The Pricing of Options and Corporate Liabilities“ von Black und Scholes vorgestellt. Robert C. Merton half bei der Herausgabe dieses Artikels.

Später im selben Jahr veröffentlichte er seinen eigenen Artikel „Theory of Rational Option Pricing“ im Bell Journal of Economics and Management Science, in dem er das mathematische Verständnis und die Anwendungen des Modells erweiterte und den Begriff „Black-Scholes-Theorie der Optionsbewertung“ prägte.

1997 erhielten Scholes und Merton den Nobel-Gedächtnispreis für Wirtschaftswissenschaften für ihre Arbeit an „einer neuen Methode zur Bestimmung des Werts von Derivaten“. Da Black zwei Jahre zuvor verstorben war, konnte er den Preis nicht entgegennehmen, da Nobelpreise nicht posthum verliehen werden. Das Nobelkomitee würdigte jedoch seine Rolle beim Black-Scholes-Modell.

Weitere Annahmen des Black-Scholes-Modells

Black-Scholes geht davon aus, dass Instrumente wie Aktien oder Futures-Kontrakte eine Lognormalverteilung der Preise aufweisen, die einem sogenannten Random Walk mit konstanter Drift (Abweichung) und Volatilität folgt. Ausgehend von dieser Annahme und unter Berücksichtigung anderer wichtiger Variablen leitet die Gleichung den Preis einer europäischen Kaufoption (Call) ab.

Darüber hinaus sagt das Modell voraus, dass der Preis von stark gehandelten Vermögenswerten einer geometrischen Brownschen Bewegung mit konstanter Drift und Volatilität folgt. Bei der Anwendung auf eine Aktienoption berücksichtigt das Modell die konstanten Kursschwankungen der Aktie, den Zeitwert des Geldes, den Strike der Option und die Restlaufzeit.

Volatility Skew

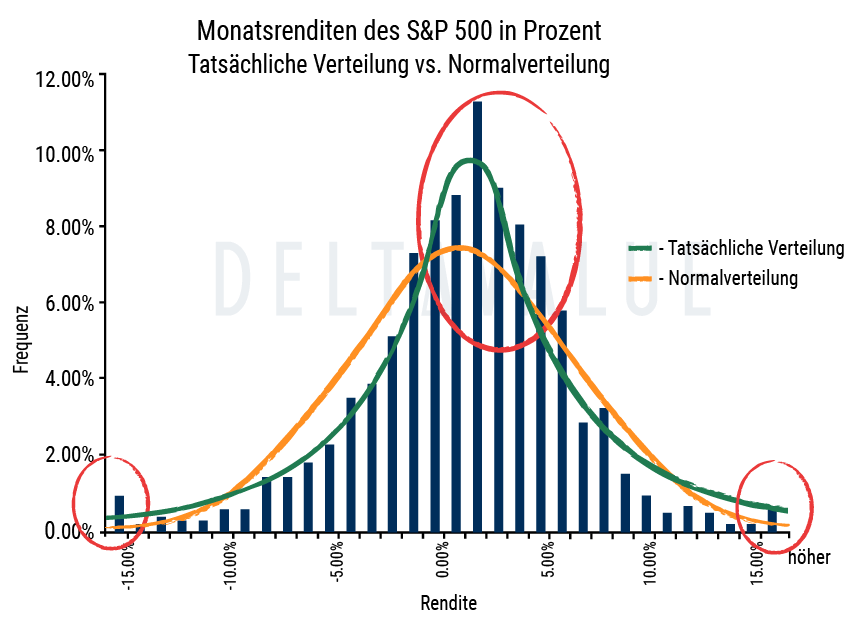
Black-Scholes geht davon aus, dass Aktienkurse einer Lognormalverteilung folgen, da Vermögenspreise nicht negativ sein können (sie sind durch Null begrenzt). Häufig wird beobachtet, dass die Preise von Vermögenswerten eine erhebliche Schiefe nach rechts und eine gewisse Kurtosis aufweisen. Dies bedeutet, dass risikoreiche Abwärtsbewegungen auf dem Markt häufiger vorkommen, als eine Normalverteilung vorhersagt.

Die Annahme lognormaler Preise für die zugrunde liegenden Vermögenswerte sollte zeigen, dass die implizite Volatilität nach dem Black-Scholes-Modell für jeden Ausübungspreis ähnlich ist.

Seit dem Börsencrash von 1987 ist die implizite Volatilität für Optionen am Geld (at the money) jedoch niedriger als für Optionen, die weiter aus dem Geld (out of the money) oder weit im Geld (in the money) sind. Der Grund für dieses Phänomen liegt darin, dass der Markt die Wahrscheinlichkeit einer hohen Volatilität auf den Märkten nach unten eingepreist.

Dies hat zum Auftreten der Volatilitätsschiefe (Volatility Skew) geführt. Wenn die implizite Volatilität für Optionen mit demselben Verfallstag in einem Diagramm dargestellt wird, kann man ein Lächeln (Volatility Smile) oder eine schiefe Form erkennen. Daher ist das Black-Scholes-Modell für die Berechnung der impliziten Volatilität nicht effizient.

Black-Scholes-Modell in der Kritik

Wie bereits erwähnt, wird das Black-Scholes-Modell nur zur Bewertung europäischer Optionen verwendet und berücksichtigt nicht, dass amerikanische Optionen vor dem Verfallsdatum ausgeübt werden könnten.

Außerdem geht das Modell von konstanten Dividenden und risikofreien Zinssätzen aus, was in der Realität nicht unbedingt der Fall ist. Das Modell geht auch davon aus, dass die Volatilität während der Laufzeit der Option konstant bleibt. Dies ist jedoch nicht der Fall, da die Volatilität mit dem Niveau von Angebot und Nachfrage schwankt.

Auch die anderen Annahmen – dass keine Transaktionskosten oder Steuern anfallen, dass der risikofreie Zinssatz für alle Laufzeiten konstant ist, dass Leerverkäufe von Wertpapieren unter Verwendung der Erlöse zulässig sind und dass es keine risikolosen Arbitragemöglichkeiten gibt – können zu Preisen führen, die von der Realität abweichen.