Vega einer Option – Definition & Erklärung
Autor: Pit Wilkens 
Inhaltlich geprüft von: Philipp-Malte Lingnau
Das Vega einer Option misst die Sensitivität des Optionspreises auf Änderungen der impliziten Volatilität. Eine höhere Volatilität führt in der Regel zu einem höheren Optionspreis, da größere Kursschwankungen wahrscheinlicher werden. Bei sinkender Volatilität verhält es sich umgekehrt. Dieser Artikel befasst sich mit dem Verhalten der Kennzahl, ihrer Interpretation und Anwendung.
🔴 Live-Webinar am 28.04.2025 um 18:30 Uhr
Ausbildung für Vermögensaufbau mit zusätzlichen monatlichen Einnahmen
Generiere ein zusätzliches regelmäßiges Einkommen an der Börse, indem du ein klares Handelssystem mit sofort umsetzbarem Investment-Wissen erlernst. Lerne Strategien kennen, die dir einen statistisch und wissenschaftlich belegbaren Vorteil an der Börse verschaffen.
Gute von schlechten Aktien unterscheiden
Profitable Aktien- und Optionsstrategien
In jeder Marktlage Geld verdienen
Plus Gratis-PDF im Webinar: Dein Start in den erfolgreichen Optionshandel
Vega einer Option – Definition
Das Vega einer Option gibt an, um wie viel sich der Optionspreis ändert, wenn die implizite Volatilität des Basiswertes (z.B. einer Aktie) um einen Prozentpunkt steigt oder fällt. Ein Vega von 0,10 bedeutet, dass eine Änderung der impliziten Volatilität um 1 Prozentpunkt den Optionspreis beispielsweise um 0,10 USD verändert.
Die Kennzahl kann gleichermaßen für Calls und Puts berechnet werden.
- Positives Vega: Eine Option mit positivem Vega (z.B. Long Calls und Long Puts) profitiert von einem Anstieg der Volatilität, da der Optionspreis steigt.
- Negatives Vega: Eine Option mit negativem Vega (z.B. Short Calls und Short Puts) profitiert von einem Rückgang der Volatilität, da sich dann der Preis der Option verringert.
Vega ist einer der sogenannten Optionsgriechen, der bei der Bewertung von Optionen relevant ist und je nach Optionsstrategie genauer betrachtet wird.
Berechnung
Vega wird, so wie alle Optionsgriechen, mit dem Black-Scholes-Modell berechnet. Die Berechnungen werden von diversen Research-Instituten und von den Emittenten der Wertpapiere sowie allen gängigen Optionshandelsplattformen mithilfe von computergestützten und automatisierten Anwendungen durchgeführt. Das Ergebnis wird als Dezimalzahl dargestellt.
Hinweis: Die Berechnung dieser Kennzahl erfolgt unter der Annahme „ceteris paribus“. Andere preisbildende Faktoren werden dabei nicht berücksichtigt.
Vega in Bezug auf Zeit und Volatilität
Diese Sensitivität wird stark durch die implizite Volatilität und die Restlaufzeit der Option bestimmt, da beide Faktoren einen erheblichen Einfluss auf das Vega haben.
Implizite Volatilität
Ein Anstieg der impliziten Volatilität führt in der Regel zu einem Anstieg der Optionspreise und umgekehrt. Diese Auswirkung wird in der folgenden Tabelle veranschaulicht.
| Option | Volatilität des Basiswertes | neuer Optionspreis | Optionspreis |
|---|---|---|---|
| Long Call | +1 % | Optionspreis + Vega-Wert | steigt |
| Long Call | – 1 % | Optionspreis – Vega-Wert | fällt |
| Long Put | + 1 % | Optionspreis + Vega-Wert | steigt |
| Long Put | – 1 % | Optionspreis – Vega-Wert | fällt |
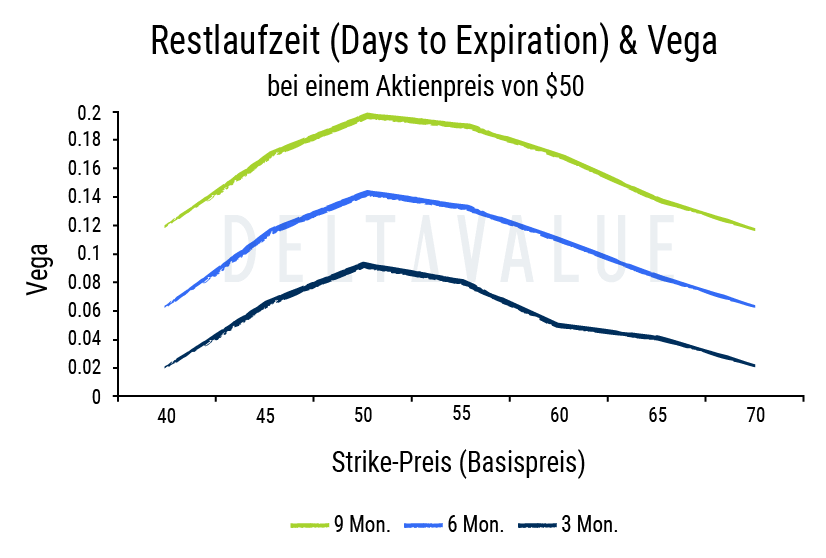
Restlaufzeit
Darüber hinaus wird Vega auch von der Restlaufzeit beeinflusst. Je höher die Restlaufzeit einer Option ist, desto höher fällt auch deren Vega-Wert aus. Die Reaktion der Option ist durch die längere Laufzeit der Option empfindlicher als bei einer Option mit kürzerer Laufzeit.
Vega in Abhängigkeit von der Geldnähe
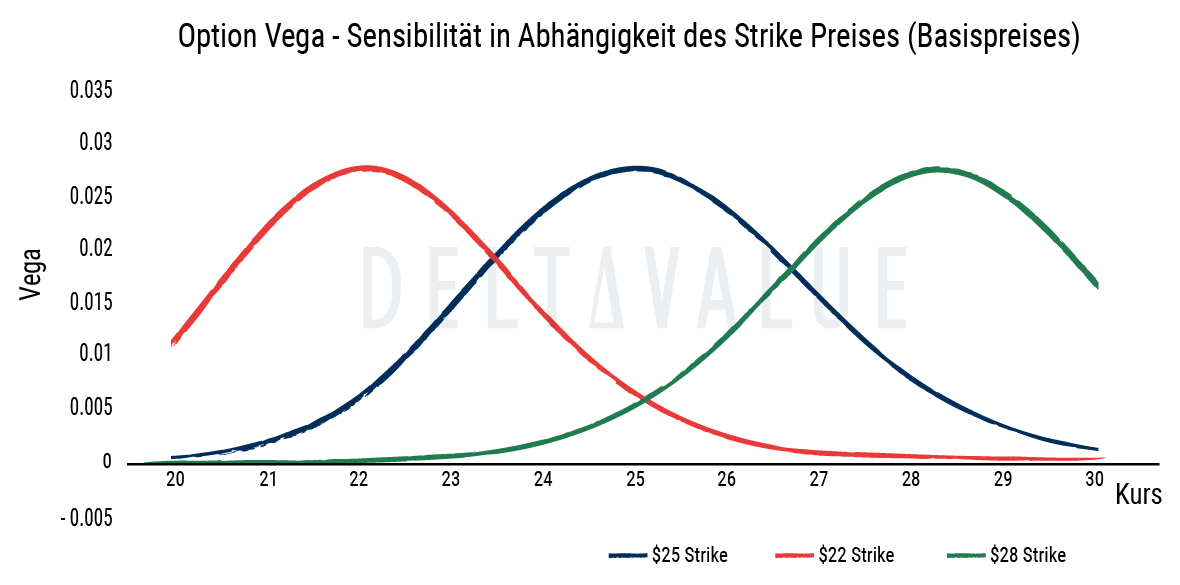
Anhand der folgenden Grafik kann gut beobachtet werden, wie das Vega einer Call-Option in Geldnähe zunimmt und wie es aus dem Geld (Out of the Money) oder im Geld (In the Money) abnimmt. Dabei ist die Veränderungsrate abhängig von der Höhe der Volatilität.
Verhalten der Kennzahl am Geld
Besonders hohe Vega-Werte sind bei Optionen am Geld (At the Money) zu beobachten. Der Optionspreis reagiert hier am empfindlichsten auf Volatilitätsänderungen. Je weiter die Option im Geld oder aus dem Geld liegt, desto eher tendiert der Wert dieser Kennzahl gegen null, da aufgrund der weiten Entfernung zum Strike-Preis die Wahrscheinlichkeit auch im Falle eines starken Anstieges der impliziten Volatilität gering ist, dass die Option im Geld fällig wird.
Beispiel: Vega einer Call-Option (Strike Preis 100 EUR)
| Kurs des Basiswertes in Euro | Optionsprämie in Euro | Volatilität | Vega |
| 102 | 3,624 | 23 % | 0,104 |
| 101 | 3,514 | 24 % | 0,11 |
| 100 | 3,4 | 25 % | 0,114 |
| 99 | 3,286 | 26 % | 0,113 |
| 98 | 3,173 | 27 % | 0,109 |
Interpretation und Bedeutung
Eine steigende Volatilität ist mit einer höheren Schwankungsbreite der Kurse und damit einem höheren Vega verbunden. Dadurch steigt, unabhängig von anderen Einflüssen, der Optionspreis. Zudem steigt die Wahrscheinlichkeit, dass die Option im Geld schließt, was eine mögliche Ausübung der Option impliziert.
Sinkt die Volatilität, sinkt der Preis der Option. Dadurch wird es für den Verkäufer (Stillhalter) günstiger, das Stillhaltergeschäft zu schließen. Außerdem sinkt die Wahrscheinlichkeit, dass die Option am Ende der Laufzeit im Geld liegt.
Unterschied zwischen Vega und anderen Optionsgriechen
Das Vega misst die Preisveränderung einer Option unter Berücksichtigung der impliziten Volatilität. Ergänzt wird die Kennzahl um drei weitere Optionsgriechen. Dazu gehört das Theta, welches Wertänderungen im Zeitverlauf misst. Das Delta gibt an, wie stark sich der Preis einer Option ändert, wenn der Kurs des Basiswertes um eine Geldeinheit steigt oder fällt. Das Gamma beschreibt die Veränderung des Deltas in Abhängigkeit der Kursveränderung des Basiswertes.
Die weiteren bekanntesten Optionsgriechen im Überblick:
Häufige Fragen
Wie wirkt sich Vega auf Optionen aus?
Bei steigender Volatilität profitieren Long-Positionen (z.B. Long Call, Long Put), bei fallender Volatilität Short-Positionen (z.B. Short Call, Short Put).
Was bedeutet Short Vega?
Short Vega bedeutet, dass eine Position negativ auf einen Anstieg der impliziten Volatilität reagiert. Beim Verkauf (Schreiben) einer Option entsteht eine Short-Position auf das Vega, da von einem Rückgang der Volatilität profitiert wird.
Kostenloses Webinar + PDF: So handelst du profitabel mit Optionen und generierst ein Zusatzeinkommen
Lerne in unserem kostenlosen Live-Webinar am 28.04.2025 um 18:30 Uhr, wie du mit dem Optionshandel ein regelmäßiges Zusatzeinkommen aufbaust. Lerne, gute von schlechten Aktien zu unterscheiden und erkenne zuverlässig überteuerte Aktienkurse. Baue dir ein zweites Einkommen auf, mit dem du unabhängig der Marktlage Geld verdienen kannst. Klicke hier, um dich für das Webinar anzumelden.