Gamma – Definition & Erklärung
Autoren: 
Philipp Berger 
Philipp-Malte Lingnau
Das Gamma einer Option misst, wie stark sich ihr Delta bei einer Preisänderung des Basiswerts um eine Einheit verändert. Ein hohes Gamma signalisiert eine hohe Empfindlichkeit des Deltas gegenüber Preisänderungen des Basiswerts. Dieser Optionsgrieche ist besonders wichtig für Händler, die ihre Delta-Positionen absichern möchten, da er Einblick in die Delta-Dynamik gibt.
🔴 Live-Webinar am 24.11.2025 um 18:30 Uhr
Ausbildung für Vermögensaufbau mit zusätzlichen monatlichen Einnahmen
Generiere ein zusätzliches regelmäßiges Einkommen an der Börse, indem du ein klares Handelssystem mit sofort umsetzbarem Investment-Wissen erlernst. Lerne Strategien kennen, die dir einen statistisch und wissenschaftlich belegbaren Vorteil an der Börse verschaffen.
Gute von schlechten Aktien unterscheiden
Profitable Aktien- und Optionsstrategien
In jeder Marktlage Geld verdienen
Plus Gratis-PDF im Webinar: Dein Start in den erfolgreichen Optionshandel
Gamma einer Option – Definition
Das Gamma einer Option gibt die Änderungsrate des Deltas bei einer Kursänderung des Basiswerts (Underlying) um eine Währungseinheit an. Bei identischen Rahmenbedingungen (z. B. Strike-Preis, Laufzeit, Volatilität) ist der Wert des Gamma für Call- und Put-Optionen gleich.
Für Long-Optionen ist Gamma positiv, für Short-Optionen hingegen negativ. Es liegt meist zwischen 0 und 1, kann bei sehr kurzer Restlaufzeit und Basiswerten mit niedrigem Preis jedoch deutlich größer als 1 sein. Die Höhe wird vor allem von der Geldnähe (Moneyness), der Restlaufzeit und der impliziten Volatilität bestimmt.
Berechnung des Gamma einer Option
Gamma wird, so wie alle Optionsgriechen, mit dem Black-Scholes-Modell berechnet. Die Berechnungen werden von diversen Research-Instituten und von den Emittenten der Wertpapiere sowie allen gängigen Optionshandelsplattformen mithilfe von computergestützten und automatisierten Anwendungen durchgeführt. Das Ergebnis wird als Dezimalzahl dargestellt.
Hinweis: Die Berechnung dieser Kennzahl erfolgt unter der Annahme „ceteris paribus“. Andere preisbildende Faktoren werden nicht berücksichtigt.
Mathematische Bedeutung des Gamma
Aus mathematischer Sicht entspricht das Gamma der zweiten partiellen Ableitung der Optionspreisformel nach dem Preis des Basiswerts. Es beschreibt somit die Änderungsrate des Deltas, welches wiederum die erste Ableitung des Optionspreises in Bezug auf den Basiswert darstellt.
Konkret bedeutet das: Verändert sich der Kurs des Basiswerts um eine sehr kleine Einheit (infinitesimale Preisänderung), so verändert sich das Delta um etwa den Betrag des Gamma. Es handelt sich dabei um eine Rate-of-change-Größe, die in der Praxis oft als Näherung „pro Preisänderung von 1 Geldeinheit“ angegeben wird. Gamma misst also die Krümmung der Optionspreisfunktion in Bezug auf den Basiswert.
Auswirkungen des Gamma auf Optionen
Steigt der Kurs des Basiswerts, nimmt das Delta von Calls um den Gamma-Wert zu, während das Delta von Puts entsprechend abnimmt. Bei fallendem Kurs verhält es sich umgekehrt. Dadurch verteuern sich Calls bei Kursanstiegen und Puts verbilligen sich (ceteris paribus). Bei Kursrückgängen ist es umgekehrt.
| Option | Kurs des Basiswerts | neues Delta | Optionspreis |
|---|---|---|---|
| Call | +1 | altes Delta + Wert des Gamma | steigt |
| Call | – 1 | altes Delta – Wert des Gamma | fällt |
| Put | + 1 | altes Delta – Wert des Gamma | fällt |
| Put | – 1 | altes Delta + Wert des Gamma | steigt |
Beispiel: Einfluss des Gamma auf den Optionspreis (Long Call)
Ein Long Call auf eine Aktie hat ein Gamma von 0,15 und ein Delta von 0,4.
- Steigt der Aktienkurs um 1 Geldeinheit (bspw. EUR), erhöht sich das Delta rechnerisch auf 0,55 (0,40 + 0,15). Die Option reagiert damit empfindlicher auf weitere Kursanstiege. Eine weitere Steigerung um 1 EUR würde nun den Optionspreis um etwa 0,55 EUR erhöhen.
- Fällt der Aktienkurs um 1 EUR, sinkt das Delta auf 0,25 (0,40 – 0,15). Ein weiterer Rückgang um 1 EUR würde den Optionspreis dann nur noch um rund 0,25 EUR verringern.
(Vereinfachte Annahme: Gamma bleibt in diesem Beispiel konstant und andere Einflussfaktoren werden ceteris paribus vernachlässigt.)
Beispiel: Einfluss des Gamma auf den Optionspreis (Long Put)
Ein Long Put auf eine Aktie hat ein Delta von –0,40 und ein Gamma von 0,15.
- Steigt der Aktienkurs um 1 Geldeinheit (bspw. EUR), erhöht sich das Delta rechnerisch auf –0,25 (–0,40 + 0,15). Der Put verliert damit bei weiteren Kursanstiegen weniger an Wert. Eine weitere Steigerung um 1 EUR würde den Optionspreis um etwa 0,25 EUR verringern statt zuvor um 0,40 EUR.
- Fällt der Aktienkurs um 1 EUR, sinkt das Delta auf –0,55 (–0,40 – 0,15). Der Put gewinnt damit bei weiteren Kursrückgängen stärker an Wert. Ein weiterer Euro Rückgang würde den Optionspreis um etwa 0,55 EUR erhöhen.
(Vereinfachte Annahme: Gamma bleibt in diesem Beispiel konstant und andere Einflussfaktoren werden ceteris paribus vernachlässigt.)
Beispiel: Einfluss des Gamma auf den Optionspreis (Short Call)
Ein Short Call hat ein Delta von –0,40 und ein Gamma von –0,15 (Gamma hat hier denselben Betrag wie im Beispiel der Long-Position, aber ein negatives Vorzeichen wegen der Short-Position).
- Steigt der Aktienkurs um 1 Geldeinheit (bspw. EUR), sinkt das Delta rechnerisch auf –0,55 (–0,40 – 0,15). Die Short-Position reagiert damit noch negativer auf weitere Kursanstiege. Eine weitere Steigerung um 1 EUR würde den Optionspreis um etwa 0,55 EUR steigen lassen.
- Fällt der Aktienkurs um 1 EUR, erhöht sich das Delta auf –0,25 (–0,40 + 0,15). Die Short-Position reagiert damit weniger negativ auf weitere Kursrückgänge. Ein weiterer Euro Rückgang würde den Optionspreis um etwa 0,25 EUR sinken lassen.
(Vereinfachte Annahme: Gamma bleibt in diesem Beispiel konstant und andere Einflussfaktoren werden ceteris paribus vernachlässigt.)
Beispiel: Einfluss des Gamma auf den Optionspreis (Short Put)
Ein Short Put hat ein Delta von 0,40 und ein Gamma von –0,15.
- Steigt der Aktienkurs um 1 Geldeinheit (bspw. EUR), sinkt das Delta rechnerisch auf 0,25 (0,40 – 0,15). Die Short-Position reagiert damit schwächer auf weitere Kursanstiege. Eine weitere Steigerung um 1 EUR würde den Optionspreis um etwa 0,25 EUR sinken lassen.
- Fällt der Aktienkurs um 1 EUR, steigt das Delta auf 0,55 (0,40 + 0,15). Die Short-Position reagiert damit empfindlicher auf weitere Kursrückgänge. Ein weiterer Euro Rückgang würde den Optionspreis um etwa 0,55 EUR steigen lassen.
(Vereinfachte Annahme: Gamma bleibt in diesem Beispiel konstant und andere Einflussfaktoren werden ceteris paribus vernachlässigt.)
Einflussfaktoren auf Gamma
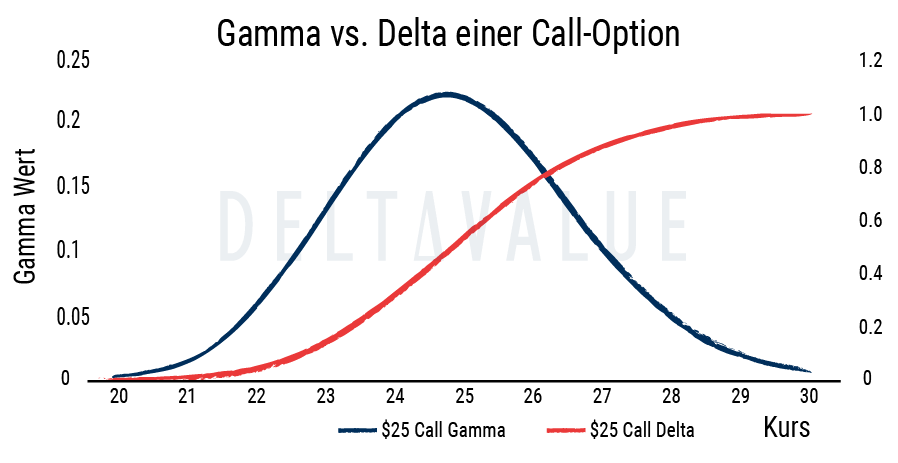
Gamma und Geldnähe (Moneyness)
Das Gamma ist bei At The Money (ATM) am höchsten, da schon kleine Kursbewegungen des Basiswerts die Wahrscheinlichkeit stark beeinflussen, ob die Option am Verfallstag In The Money (ITM) oder Out of The Money (OTM) endet.
Entfernt sich der Kurs vom ATM-Bereich, verändert sich das Delta nur noch langsam – Gamma sinkt und tendiert bei stark ITM- oder OTM-Optionen gegen null. Diese geringe Preissensitivität wird im Gamma Hedging gezielt genutzt.
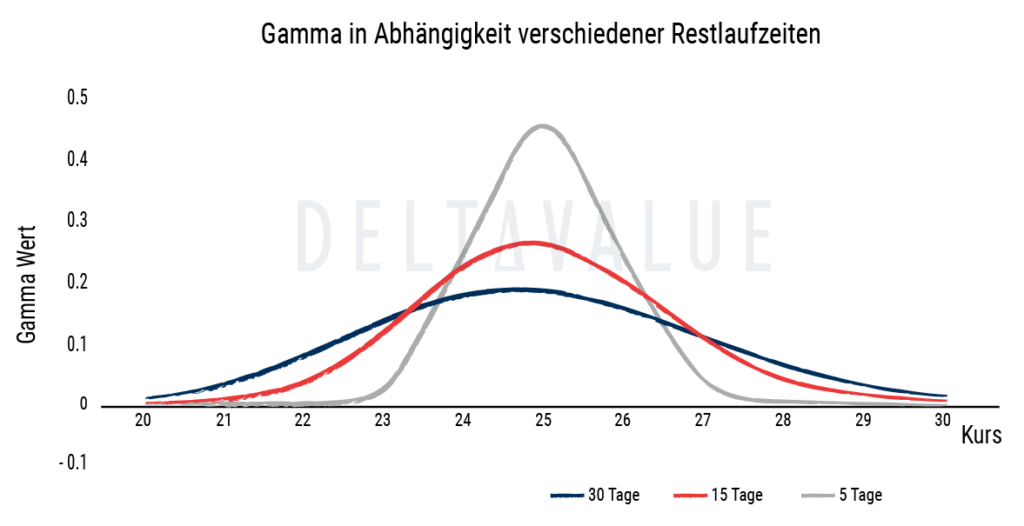
Gamma und der Einfluss der Restlaufzeit
Das Gamma einer ATM-Option steigt, je kürzer ihre Restlaufzeit ist. Bei nur wenigen Tagen bis zur Fälligkeit können schon kleinste Kursänderungen den Optionspreis stark beeinflussen, was auch als Gamma-Risiko bekannt ist.
Die Grafik zeigt diesen Effekt für einen Strike von 25 USD: Optionen mit 5 Tagen Restlaufzeit (grau) weisen deutlich höhere Gamma-Spitzen auf als solche mit 15 (rot) oder 30 Tagen (blau).
Für eine einzelne ATM-Option lässt sich der zeitliche Verlauf des Gamma schematisch darstellen: Je kürzer die Restlaufzeit, desto stärker steigt das Gamma an.
Gamma und implizite Volatilität
Gamma hat eine invertierte Beziehung zur impliziten Volatilität. Wenn die implizite Volatilität ansteigt, steigen die Optionspreise. Dadurch verringert sich Gamma, da sich Änderungen des Basiswertpreises weniger stark auf das Delta der Option auswirken, wenn noch ein großer extrinsischer Wert vorhanden ist.
Umgekehrt steigt Gamma, wenn die implizite Volatilität sinkt, da der Optionspreis empfindlicher auf Veränderungen des Basiswerts reagiert.
Beispiel zur Gamma-Entwicklung
Am Beispiel einer Call-Option mit einem Strike-Preis von 55 €, 30 Tagen Restlaufzeit und 20 % impliziter Volatilität zeigt sich: Gamma ist am höchsten, wenn die Option am Geld (ATM) notiert.
Befindet sich die Option dagegen deutlich im Geld oder aus dem Geld, nimmt Gamma ab. Nach dem Überschreiten des Break-even-Punkts sinkt Gamma kontinuierlich. In der Praxis beeinflussen jedoch auch Faktoren wie der Zeitwert den Optionspreis – nicht nur der Kurs des Basiswerts.
| Kurs des Basiswertes | Delta | Gamma | Neues Delta |
| 40 | 0,12 | 0,015 | 0,135 |
| 45 | 0,28 | 0,025 | 0,305 |
| 50 | 0,43 | 0,035 | 0,465 |
| 55 | 0,50 | 0,040 | 0,540 |
| 60 | 0,57 | 0,035 | 0,605 |
| 65 | 0,72 | 0,025 | 0,745 |
| 70 | 0,88 | 0,015 | 0,895 |
Was ist Gamma Hedging?
Ein Portfolio mit einem hohen positiven oder negativen Gamma zeigt starke Schwankungen im Delta, sobald sich der Kurs des Basiswerts verändert. Um dieses Risiko zu begrenzen, setzen vor allem Market Maker und institutionelle Anleger Gamma-Hedging-Strategien ein.
Ein gamma-neutrales Portfolio reagiert nicht auf Änderungen des Deltas, wenn sich der Basiswertkurs bewegt. Market Maker streben oft Gamma-Neutralität an, um bei großen Optionsbeständen das Risiko starker Kursschwankungen zu reduzieren.
Beispielsweise kann ein Übergewicht an Call-Optionen zu einem übermäßig positiven Gamma führen. Durch den Zukauf von Put-Optionen lässt sich die Gamma-Exponierung verringern und die Preissensitivität gegenüber dem Basiswert ausgleichen.
Hinweis: Während ein Delta-Hedging durch Kauf oder Verkauf des Basiswerts oder von Optionen erfolgen kann, wird ein Gamma-Hedging ausschließlich über Optionen umgesetzt.
Das Phänomen des Gamma Squeeze
Ein Gamma Squeeze entsteht, wenn eine starke Kursbewegung des Basiswerts Market Maker zwingt, große Mengen des Basiswerts zu kaufen oder zu verkaufen, um ihre Optionspositionen abzusichern.
Übernimmt ein Market Maker die Gegenposition zu einer Option – etwa beim Verkauf eines kurzfristigen Calls auf eine volatile „Meme-Aktie“ – ist er steigenden Kursen ausgesetzt. Um das Risiko zu reduzieren, kauft er den Basiswert, sobald der Kurs steigt, und stellt damit Delta-Neutralität her.
Steigt der Kurs weiter, muss er erneut zukaufen, um das Delta anzupassen. Dieser fortgesetzte Kaufdruck kann die Aufwärtsbewegung verstärken und so eine Kursrallye auslösen – der typische Mechanismus hinter einem Gamma Squeeze.
Exkurs: Die Optionsgriechen
In der Finanzmathematik werden Sensitivitätskennzahlen für Derivate oft als „Griechen“ bezeichnet. Sie bilden eine wichtige Grundlage für das Risikomanagement, da sie die Auswirkungen einzelner Rahmenbedingungen auf den Optionspreis klar isolieren und bewerten.
Weitere Optionsgriechen im Überblick:
- Delta gibt an, wie sich der Optionspreis verändert, wenn der Basiswert um eine Geldeinheit schwankt.
- Theta ist ein Maß für den Zeitwertverlust. Es gibt an, um welchen Betrag der Optionspreis pro verstrichenen Tag sinkt.
- Vega misst den Einfluss der impliziten Volatilität auf den Optionspreis.
- Rho quantifiziert, wie empfindlich der Optionswert auf Veränderungen des risikofreien Zinssatzes reagiert.
- Omega ist eine Hebelkennzahl, die die prozentuale Veränderung des Optionspreises im Verhältnis zur prozentualen Veränderung des Basiswerts angibt.
Kostenloses Webinar + PDF: So handelst du profitabel mit Optionen und generierst ein Zusatzeinkommen
Lerne in unserem kostenlosen Live-Webinar am 24.11.2025 um 18:30 Uhr, wie du mit dem Optionshandel ein regelmäßiges Zusatzeinkommen aufbaust. Lerne, gute von schlechten Aktien zu unterscheiden und erkenne zuverlässig überteuerte Aktienkurse. Baue dir ein zweites Einkommen auf, mit dem du unabhängig der Marktlage Geld verdienen kannst. Klicke hier, um dich für das Webinar anzumelden.