Bewertung von Optionen – Erklärung & Formel

Put-Call Parität

Grundsätzlich sei vorweg erwähnt, dass zwischen Put- und Callpreisen europäischer Optionen auf nicht-dividendenzahlende Basiswerte eine mathematische Beziehung besteht, die als Put-Call Parität bezeichnet wird. Diese besagt, dass der Preis eines Puts aus dem Preis eines Calls abgeleitet werden kann und vice versa, sofern Strike und Restlaufzeit identisch sind.

Dieser Zusammenhang ergibt sich aus der sog. Put-Call Paritätsgleichung:

Black-Scholes Modell

Mit dem Black-Scholes Modell, auch bekannt als Black-Scholes-Merton Modell, gelang den Wissenschaftlern Fischer Black, Myron Scholes und Robert Merton Anfang der 1970er-Jahre der entscheidende Durchbruch zur numerischen Bewertung von Optionen.

Ihnen ist es zu verdanken, dass Anlegern heute ein breites Angebot an handelbaren Optionen zur Verfügung steht. Das Black-Scholes Modell stellt die eigentliche Grundlage für die heutige Bewertung von Optionen und Optionsscheinen dar.

Funktionsweise

Grundsätzlich dient das Black-Scholes Modell der Bewertung europäischer Optionen auf Basis eines stochastischen Prozesses für den Preis des Underlyings. Es wird davon ausgegangen, dass der Preis des Basiswertes einer geometrischen Brownschen Bewegung folgt.

Daraus ergibt sich, dass die Preise zu einem zukünftigen Zeitpunkt lognormalverteilt sind bzw. die logarithmierten Renditen eine Normalverteilung aufweisen. Unter Verwendung dieser Annahme, und unter Berücksichtigung weiterer Prämissen sowie Variablen, kann mit dem Modell der Preis einer Option und eines Optionsscheins abgeleitet werden.

Grundannahmen des Black-Scholes Modells im Überblick

Binomialmodell

Das Binomialmodell gehört ebenfalls zu den bekannten Bewertungsmodellen. Der Optionspreis wird hierbei mithilfe von Binomialbäumen ermittelt.

Grundsätzlich besagt das Binomialmodell, dass der Preis des Underlying zwischen zwei Zeitpunkten entweder um den Faktor u (u wie up) steigen, oder um den Faktor d (d wie down) fallen kann. Dabei wird ein diskreter stochastischer Prozess zugrunde gelegt, d.h. das Modell unterliegt einem diskontinuierlichen Prozess mit abzählbaren Zeitabständen und zufälligen Vorgängen.

Dieser Grundsatz unterscheidet das Binomialmodell vom Black-Scholes Modell, dem ein kontinuierlicher stochastischer Prozess zugrunde liegt, d.h. das Modell basiert auf einem stetigen Prozess mit nicht abzählbaren Zeitabständen und zufälligen Vorgängen.

Es handelt sich daher um ein diskretes Modell, das in seiner einfachen Grundform auf einer sehr einfachen Betrachtung des Preisprozesses des Basiswertes (Underlying) basiert und den folgenden Annahmen zugrunde liegt:

* In erweiterten Varianten können Dividendenzahlungen jedoch berücksichtigt werden.

Nachteile bei der Bewertung von Optionen

Obwohl das Black-Scholes Modell als auch das Binomialmodell zur Bewertung von Optionen und Optionsscheinen herangezogen werden, weisen beide Modelle Kritikpunkte auf.

Beispielsweise fallen in der praktischen Anwendung Steuern und Transaktionskosten an, die per Annahme in den Modellen keine Berücksichtigung finden. Gleiches gilt für die Volatilität und das Zinsniveau. Beide Variablen sind in der Realität nicht zwangsläufig konstant, insbesondere die Volatilität nicht.

Kritik am Black-Scholes Modell

Beim Black-Scholes Modell sollte auch Folgendes kritisch betrachtet werden:

• Dividendenzahlungen werden über die Laufzeit als konstant betrachtet. In der Realität unterliegen die Auszahlungen Schwankungen.
• Für die exakte Bewertung amerikanischer Optionen existiert im Regelfall keine geschlossene Black-Scholes Formel. Mithilfe des Black-Scholes Modell kann daher allenfalls eine Näherung des Werts amerikanischer Optionen erfolgen. In der Praxis werden hierfür häufig numerische Verfahren wie Binomialmodelle oder Approximationsverfahren verwendet. Insbesondere bei Put-Optionen sowie bei Calls auf dividendenzahlende Basiswerte kann die Möglichkeit der vorzeitigen Ausübung wertrelevant sein.
• Aktienkurse sind in der Realität nicht lognormalverteilt.

Volatility-Smile und Volatility-Skew

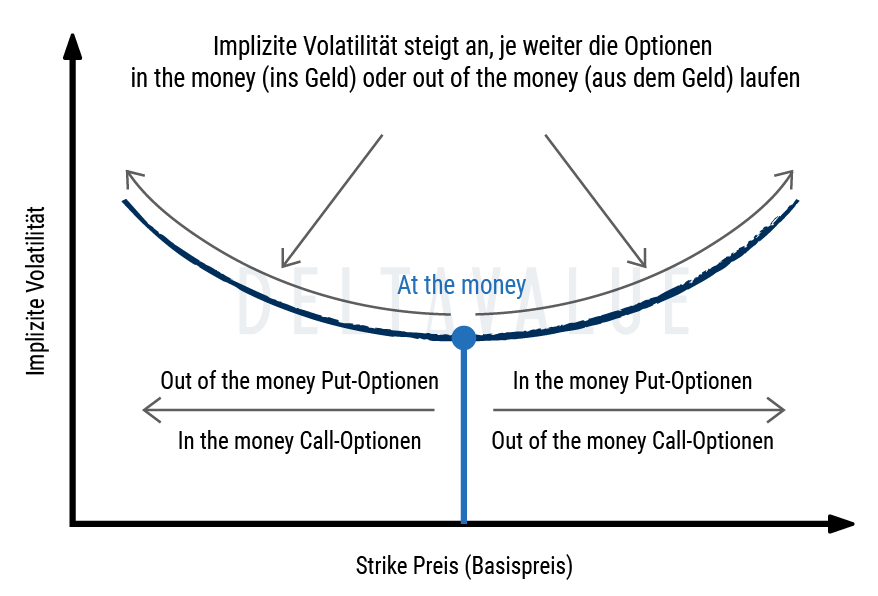
Der größte Widerspruch der Black-Scholes Modellannahmen gegenüber der Kapitalmarktpraxis, liegt in der Annahme, dass die Volatilität als konstant angenommen wird. Bei der Ableitung der Black-Scholes Formel zur Berechnung der impliziten Volatilität kann jedoch aufgezeigt werden, dass bei der Betrachtung der impliziten Volatilität von Optionen und Optionsscheinen auf dasselbe Underlying mit derselben oder ähnlichen Laufzeit, jedoch abweichenden Strikes, in der Praxis häufig keine konstante Struktur, sondern ein vom Strike abhängiger Verlauf beobachtet werden kann.

Je nach Markt und Underlying kann sich diese Struktur als sog. Volatility-Smile oder als asymmetrische Volatility-Skew zeigen. Während bei manchen Märkten ein eher symmetrischer Smile beobachtet werden kann, weisen insbesondere Aktienoptionen häufig eine asymmetrische Struktur auf, bei der aus dem Geld liegende Put-Optionen eine höhere implizite Volatilität aufweisen als vergleichbare Call-Optionen.

Kritik am Binomialmodell

Beim Binomialmodell sollten folgende Punkte kritisch betrachtet werden:

• Aktienkurse folgen einer stetigen Preisquotierung.
• Dividenden werden im einfachen Grundmodell zunächst nicht berücksichtigt.
• Die im Modell verwendeten risikoneutralen Wahrscheinlichkeiten stellen kein reales Anlegerverhalten dar, sondern ein Bewertungsmaß im No-Arbitrage-Rahmen.

Letztlich muss jedoch hervorgehoben werden, dass sich die beiden Modelle bei einfachen Derivaten gut zur Preisbestimmung eignen und daher praktikabel sind. Bei komplexeren Derivaten findet verstärkt die sog. Monte-Carlo Simulation Anwendung.