Die Kurtosis, auch “Wölbung” genannt, ist ein statistisches Maß, das zur Beschreibung der Verteilung von Daten verwendet wird. Während die Schiefe die Extremwerte an einem der beiden Ränder einer Verteilung unterscheidet, misst die Kurtosis die Extremwerte an beiden Rändern der Verteilung. Die Kurtosis kann ein wertvolles Instrument für das Risikomanagement an der Börse sein, da sie anzeigt, ob eine Anlage, wie z. B. Aktien, anfällig für extreme Ergebnisse ist.
🔴 Live-Webinar am 11.12.2023 um 18:30 Uhr
Ausbildung für Vermögensaufbau mit zusätzlichen monatlichen Einnahmen
Generiere ein zusätzliches regelmäßiges Einkommen an der Börse, indem du ein klares Handelssystem mit sofort umsetzbarem Investment-Wissen erlernst. Lerne Strategien kennen, die dir einen statistisch und wissenschaftlich belegbaren Vorteil an der Börse verschaffen.
Gute von schlechten Aktien unterscheiden
Profitable Aktien- und Optionsstrategien
In jeder Marktlage Geld verdienen
Plus Gratis-PDF im Webinar: Dein Start in den erfolgreichen Optionshandel
Kurtosis – Definition
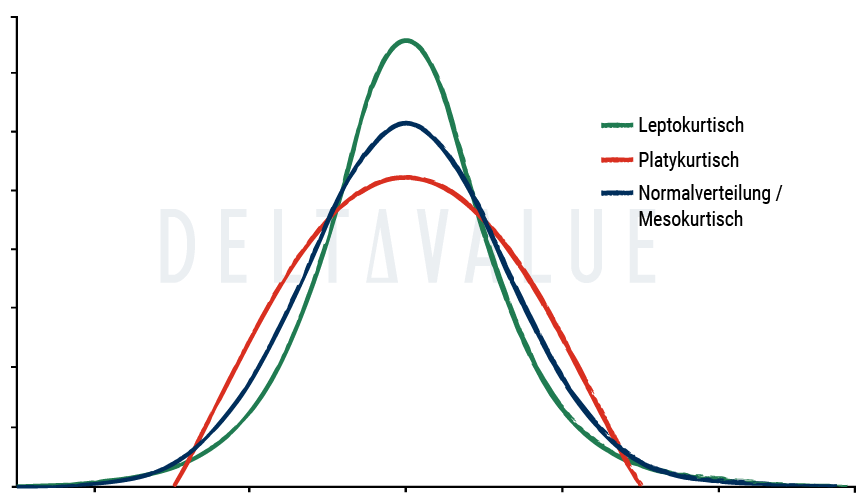
Die Kurtosis beschreibt, ob die Spitze einer Verteilung flacher oder spitzer ist als die Mitte einer Normalverteilung. Für die Kurtosis wird die Anzahl der Datenpunkte am äußeren Rand einer Verteilung gemessen und mit dem Rest der Verteilung verglichen. Das Ergebnis kann positiv (leptokurtische Verteilung), negativ (platykurtische Verteilung) oder nahe null (mesokurtische Verteilung) sein.
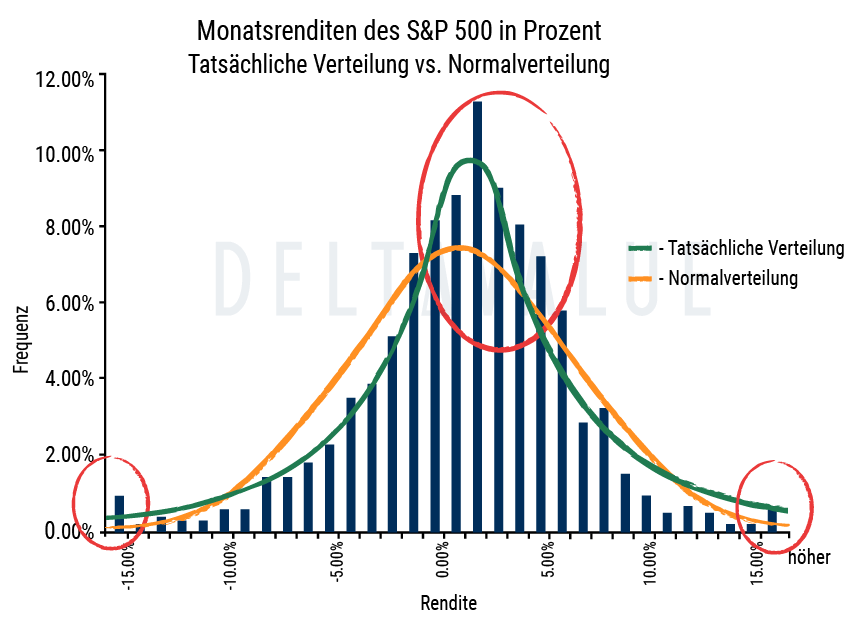
- Leptokurtische Verteilung: Verteilungen mit hoher (positiver) Kurtosis weisen Daten auf, die an den Enden mehr Häufigkeit aufweisen als es bei einer Normalverteilung der Fall wäre (sog. “Fat Tails”).
- Platykurtische Verteilung: Verteilungen mit geringer (negativer) Kurtosis weisen Daten auf, die an den Rändern im Allgemeinen weniger extrem sind als bei einer Normalverteilung.
- Mesokurtische Verteilung: Datenverteilungen mit einer Wölbung nahe null entsprechen in etwa die Normalverteilung.
Bedeutung der Kurtosis
Die Kurtosis ist eine statistische Kennzahl für das kombinierte Gewicht der Enden einer Verteilung im Verhältnis zum Zentrum der Verteilung. Sie wird manchmal mit einem Maß für die Spitzenhaftigkeit (engl. “peakedness”) einer Verteilung verwechselt. Die Kurtosis ist jedoch ein Maß, das die Form der Enden einer Verteilung im Verhältnis zu ihrer Gesamtform beschreibt. Eine Verteilung kann beispielsweise unendlich spitz sein und eine geringe Wölbung aufweisen oder vollkommen flach sein und eine unendliche Kurtosis aufweisen.
Eine Kurtosis misst also die „Endenhöhe“, nicht die „Spitzenhöhe“.
Für Anleger bedeuten überdurchschnittlich hohe Kurtosis bei Kapitalmarktrenditen, dass extreme Renditen (entweder positiv oder negativ) häufiger auftreten können, als bei einer Normalverteilung zu erwarten wäre. Dieses Phänomen wird als Kurtosis-Risiko, Tail-Risiko (engl. “Tail Risks”) bezeichnet. Entsprechend bedeutet eine geringe Wölbung, dass Ausreißer seltener auftreten können.
Kategorien der Kurtosis
Es gibt drei Kategorien von Kurtosis, die durch einen Datensatz angezeigt werden können. Alle Wölbungsmaße werden mit einer Standard-Normalverteilung oder einer Glockenkurve verglichen.
Mesokurtische Verteilung
Die erste Kategorie der Kurtosis ist die mesokurtische Verteilung. Diese Verteilung hat eine ähnliche Kurtosisstatistik wie die Normalverteilung, d. h. die Extremwerte der Verteilung sind ähnlich wie bei der Normalverteilung. Wenn ein Datensatz mit annähernd normaler Verteilung in einem Histogramm dargestellt wird, zeigt das Histogramm eine Glockenkurve, wobei die meisten Daten innerhalb von drei Standardabweichungen (plus oder minus) vom Mittelwert liegen.
Leptokurtische Verteilung
Die zweite Kategorie ist eine leptokurtische Verteilung. Die Vorsilbe „lepto-“ bedeutet „dünn“, wodurch die Form einer leptokurtischen Verteilung leichter zu merken ist. Jede leptokurtische Verteilung weist eine größere Kurtosis auf als eine mesokurtische Verteilung. Charakteristisch für diese Verteilung sind lange Extremitäten (Ausreißer).
Wenn eine hohe Wölbung vorliegt, reichen die Enden weiter als die drei Standardabweichungen der normalen glockenförmigen Verteilung im Histogramm. Die „Dünnheit“ einer leptokurtischen Verteilung ist eine Folge der Ausreißer, die die horizontale Achse des Histogramms strecken und den Großteil der Daten in einem schmalen („dünnen“) vertikalen Bereich erscheinen lassen.
Daher werden leptokurtische Verteilungen manchmal als „auf den Mittelwert konzentriert“ bezeichnet, aber das relevantere Problem (insbesondere für Anleger) ist, dass es gelegentlich extreme Ausreißer gibt, die dieses „konzentrierte“ Erscheinungsbild verursachen. Beispiele für leptokurtische Verteilungen sind die T-Verteilungen mit kleinen Freiheitsgraden.
Platykurtische Verteilung
Der letzte Verteilungstyp ist eine platykurtische Verteilung. Die Vorsilbe „platy-“ bedeutet „breit“ und soll eine kurze und breit aussehende Spitze beschreiben. Diese Verteilungen haben kurze Enden (weniger Ausreißer). Bei einer geringen Wölbung sind die Enden daher kurzer als bei der Normalverteilung im Histogramm.
Gleichmäßige Verteilungen sind platykurtisch und haben breite Spitzen. Die Beta-Verteilung ist ebenfalls platykurtisch und hat eine unendliche Spitze. Der Grund dafür, dass diese beiden Verteilungen platykurtisch sind, ist, dass ihre Extremwerte geringer sind als die der Normalverteilung.
Für Anleger sind platykurtische Renditeverteilungen stabil und vorhersehbar in dem Sinne, dass es selten (wenn überhaupt) zu extremen (Ausreißer-)Renditen kommen wird.
Kostenloses Webinar + PDF: So handelst du profitabel mit Optionen und generierst ein Zusatzeinkommen
Lerne in unserem kostenlosen Live-Webinar am 11.12.2023 um 18:30 Uhr, wie du mit dem Optionshandel ein regelmäßiges Zusatzeinkommen aufbaust. Lerne, gute von schlechten Aktien zu unterscheiden und erkenne zuverlässig überteuerte Aktienkurse. Baue dir ein zweites Einkommen auf, mit dem du unabhängig der Marktlage Geld verdienen kannst. Klicke hier, um dich für das Webinar anzumelden.