Rho einer Option – Definition & Beispiel
Das Rho einer Option gibt an, wie empfindlich der Optionspreis auf eine Änderung des risikofreien Zinssatzes (z. B. von US-Staatsanleihen) um 1 % reagiert. Darüber hinaus eignet sich die Sensitivitätskennzahl, um das Gesamtpotenzial eines gesamten Optionsportfolios gegenüber Änderungen des risikofreien Zinssatzes zu bewerten, da sie sich additiv über Positionen aufsummieren lässt.
🔴 Live-Webinar am 01.09.2025 um 18:30 Uhr
Ausbildung für Vermögensaufbau mit zusätzlichen monatlichen Einnahmen
Generiere ein zusätzliches regelmäßiges Einkommen an der Börse, indem du ein klares Handelssystem mit sofort umsetzbarem Investment-Wissen erlernst. Lerne Strategien kennen, die dir einen statistisch und wissenschaftlich belegbaren Vorteil an der Börse verschaffen.
 Gute von schlechten Aktien unterscheiden
Gute von schlechten Aktien unterscheiden
Profitable Aktien- und Optionsstrategien
In jeder Marktlage Geld verdienen
Plus Gratis-PDF im Webinar: Dein Start in den erfolgreichen Optionshandel
Rho einer Option – Definition
Das Rho einer Option misst, wie stark sich der Preis einer Option ändert, wenn der risikofreie Zinssatz um 1 Prozentpunkt steigt oder fällt, bei konstanten anderen Faktoren. Beispielsweise ein Rho von 1 bedeutet, dass der Optionspreis sich um denselben Prozentsatz wie der Zinssatz ändert.
Berechnung des Rho einer Option
Wie die anderen Sensitivitätskennzahlen wird auch Rho im (erweiterten) Black-Scholes-Modell berechnet. In der Praxis übernehmen Händler- und Emittenten-Systeme diese Berechnung automatisch. Das Ergebnis wird als Dezimalzahl ausgegeben (z. B. Rho = 0,45 entspricht einer Preisänderung von ca. 0,45 EUR je 1 %-Punkt Zinsbewegung).
Mathematische Bedeutung des Rho
Aus mathematischer Sicht entspricht Rho der partiellen Ableitung der Optionspreisformel nach dem stetigen risikofreien Zinssatz 𝑟. Es misst somit, wie empfindlich der Optionspreis auf kleine Änderungen des Zinssatzes reagiert, während alle anderen Parameter (Kurs, Volatilität, Laufzeit usw.) konstant gehalten werden.
Konkret bedeutet das: Erhöht oder senkt sich der Zinssatz um eine sehr kleine Einheit (infinitesimale Zinsänderung), so verändert sich der Optionspreis um etwa den Betrag des Rho. Es handelt sich dabei um eine Rate-of-change-Größe, die in der Praxis oft als Näherung „pro 1 % Zinsänderung“ angegeben wird. Rho misst also die Steigung der Optionspreisfunktion in der r-Dimension an.
Auswirkungen des Rho auf Optionen
Rho ist bei Call-Optionen positiv und bei Put-Optionen negativ. Steigende Zinsen erhöhen den Wert von Calls und verringern den Wert von Puts. Bei fallenden Zinsen verhält es sich umgekehrt (ceteris paribus).
| Option | Zinssatz (r) | Preisänderung (theoretisch) | Optionspreis |
|---|---|---|---|
| Call | +1 %-Punkt | ρ×Δr (ρ > 0) | steigt |
| Call | −1 %-Punkt | ρ×Δr (ρ > 0) | fällt |
| Put | +1 %-Punkt | ρ×Δr (ρ < 0) | fällt |
| Put | −1 %-Punkt | ρ×Δr (ρ < 0) | steigt |
Einflussfaktoren auf Rho
Rho und Geldnähe (Moneyness)
Rho ist bei Optionen in der Regel am größten, wenn sie tief In The Money sind. At The Money (ATM) ist Rho meist moderat, weit Out of The Money (OTM) nähert es sich null.
Rho und der Einfluss der Restlaufzeit
Rho steigt mit der Restlaufzeit, daher reagieren LEAP-Optionen deutlich stärker auf Zinsänderungen als kurz laufende Optionen. Bei sehr kurzer Laufzeit ist Rho meist klein (außer bei Optionen Deep In The Money).
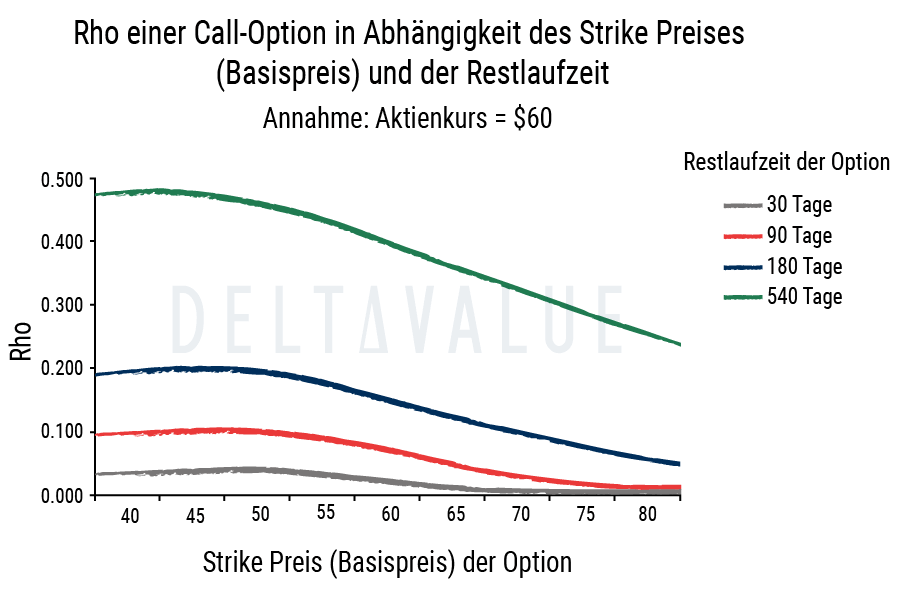
Der Verlauf des Rho von Call-Optionen mit unterschiedlichen Restlaufzeiten kann anhand des folgenden Diagramms visualisiert werden: Die Kurven für 30/90/180/540 Tage zeigen, dass Rho mit zunehmender Restlaufzeit steigt, jedoch mit steigendem Strike fällt. Am stärksten ist dieser Effekt bei tief im Geld liegenden Calls (niedrige Strikes).
Beispiel zur Rho-Entwicklung
Die mathematische Herleitung von Rho ist für Praktiker meist zweitrangig. Wichtig ist zu verstehen, dass sich Rho auf Änderungen des risikolosen Zinssatzes bezieht. Dieser Zinssatz orientiert sich an sicheren Referenzzinsen (in den USA z. B. an US-Treasuries, im Euro-Raum an €STR oder Euribor).
Beispiel 1 – Call-Option (Rho positiv)
| Optionsart | Strike-Preis | Rho | Risikoloser Zins |
|---|---|---|---|
| Call Option | 4 EUR | 0,25 | 1 % |
Steigt der Zinssatz um 1 %-Punkt auf 2 %, erhöht sich der Optionspreis um 0,25 EUR auf 4,25 EUR.
Beispiel 2 – Put-Option (Rho negativ)
| Optionsart | Strike-Preis | Rho | Risikoloser Zins |
|---|---|---|---|
| Put Option | 9 EUR | -0,35 | 1 % |
Sinkt der Zinssatz um 1 %-Punkt auf 0 %, steigt der Optionspreis um 0,35 EUR auf 9,35 EUR. Zum Vergleich: Die Call-Option aus Beispiel 1 würde bei diesem Zinsrückgang um 0,25 EUR auf 3,75 EUR fallen.
Warum beeinflussen die Zinsen den Optionspreis?
Der zentrale Grund ist der sogenannte Cost of Carry. Er beschreibt die Kosten (bzw. Erträge), die entstehen, wenn man den Basiswert (Underlying) bis zum Verfall „trägt“.
Bei Aktien besteht der Carry im Wesentlichen aus Finanzierungskosten (Zins) minus erwarteter Dividenden. Steigen die Zinsen, wird das Halten/Finanzieren teurer und gleichzeitig sinkt der heutige Wert eines künftig zu zahlenden Strikes (Abzinsung). Ergebnis ceteris paribus: Calls werden tendenziell teurer, Puts tendenziell günstiger.
Unterschiede bei anderen Underlyings
Optionen auf Futures
Bei Optionen auf Futures gibt es keinen sofortigen Geldfluss für den Basiswert (der Future ist ja selbst ein Termingeschäft). Deshalb wirken Zinsänderungen nicht über Finanzierungskosten des Underlyings, sondern nur über die Abzinsung des künftigen Auszahlungsbetrags.
Praktisch kann es jedoch indirekte Effekte geben:
- Aktienindex-Futures: Steigende Zinsen erhöhen den theoretischen Futures-Preis (da die Opportunitätskosten für das gebundene Kapital steigen und Dividendenzahlungen erst später anfallen).
- Rohstoff-Futures: Hier können Zinsen über Lagerkosten („Cost of Carry“) oder Finanzierungskosten der Bestände wirken. Höhere Zinsen verteuern typischerweise das Halten physischer Lagerbestände, was sich im Futures-Preis widerspiegeln kann.
- Zins- und Währungsfutures: Hier ist die Abhängigkeit zu Zinsen naturgemäß direkt, da der zugrunde liegende Future selbst ein Zins- oder Wechselkursversprechen darstellt.
In diesen Fällen führt eine Zinsänderung zu einer Anpassung des beobachteten Futures-Preises, was sich wiederum indirekt auf den Optionspreis auswirkt. Dies geschieht jedoch nicht als klassischer Rho-Effekt, sondern als Delta-Effekt (Preisänderung des Basiswerts).
FX-Optionen (Währungsoptionen)
Bei FX-Optionen ist Rho zweigeteilt: Es gibt einen Zinssatz für die Heimatwährung (Domestic Interest Rate) und einen für die Fremdwährung (Foreign Interest Rate).
- Erhöht sich der heimische Zinssatz, wirkt das ähnlich wie bei einem Aktien-Call (positiv auf Calls, negativ auf Puts, wenn auf den Wechselkurs in heimischer Währung notiert).
- Erhöht sich der ausländische Zinssatz, kehrt sich das Vorzeichen um.
Formelmäßig steckt dieser Effekt im Garman–Kohlhagen-Modell.
Exkurs: Die Optionsgriechen
In der Finanzmathematik werden Sensitivitätskennzahlen für Derivate oft als „Griechen“ bezeichnet. Sie bilden eine wichtige Grundlage für das Risikomanagement, da sie die Auswirkungen einzelner Rahmenbedingungen auf den Optionspreis klar isolieren und bewerten.
Weitere Optionsgriechen im Überblick:
- Delta gibt an, wie sich der Optionspreis verändert, wenn der Basiswert um eine Geldeinheit schwankt.
- Gamma misst den Einfluss der Kursänderung auf das Delta.
- Omega ähnelt dem Delta, misst aber die prozentuale Änderung des Optionspreises im Verhältnis zur prozentualen Änderung des Basiswertpreises.
- Theta ist ein Maß für den Zeitwertverlust. Es gibt an, um welchen Betrag der Optionspreis pro verstrichenen Tag sinkt.
- Vega misst den Einfluss der impliziten Volatilität auf den Optionspreis.
Kostenloses Webinar + PDF: So handelst du profitabel mit Optionen und generierst ein Zusatzeinkommen
 Lerne in unserem kostenlosen Live-Webinar am 01.09.2025 um 18:30 Uhr, wie du mit dem Optionshandel ein regelmäßiges Zusatzeinkommen aufbaust. Lerne, gute von schlechten Aktien zu unterscheiden und erkenne zuverlässig überteuerte Aktienkurse. Baue dir ein zweites Einkommen auf, mit dem du unabhängig der Marktlage Geld verdienen kannst. Klicke hier, um dich für das Webinar anzumelden.
Lerne in unserem kostenlosen Live-Webinar am 01.09.2025 um 18:30 Uhr, wie du mit dem Optionshandel ein regelmäßiges Zusatzeinkommen aufbaust. Lerne, gute von schlechten Aktien zu unterscheiden und erkenne zuverlässig überteuerte Aktienkurse. Baue dir ein zweites Einkommen auf, mit dem du unabhängig der Marktlage Geld verdienen kannst. Klicke hier, um dich für das Webinar anzumelden.