Terminstrukturkurve – Erklärung

Terminstrukturkurve – Definition

Die Terminstrukturkurve stellt ein zentrales Instrument für die Bewertung von Warenterminprodukten wie Futures dar. Mit Hilfe der Terminstrukturkurve ist die visuelle Darstellung der Preise einzelner Futures-Kontrakte, die sich auf denselben Basiswert (beispielsweise Rohstoffe oder Indizes) beziehen, in Abhängigkeit zu ihrer Laufzeit bis zur Fälligkeit möglich.

Aufbau

Die Terminstrukturkurve ist in ihrem Aufbau an die Zinsstrukturkurve angelehnt, muss von dieser aber differenziert werden, da sich die Zinsstrukturkurve auf die Darstellung von Zinssätzen bzw. Renditen bezieht.

Normalfall

Im idealtypischen Normalfall verläuft die Terminstrukturkurve asymptotisch nach oben. Das bedeutet, je länger die Laufzeit des Futures-Kontrakts, desto höher ist der Preis. Da es sich um einen asymptotischen Verlauf handelt, nimmt der Preisanstieg im idealtypischen Normalfall kontinuierlich ab — die Terminstrukturkurve wird flacher. Ihr liegt also kein linearer Verlauf zugrunde.

Invertiert

Da die Struktur der Terminstrukturkurve im Wesentlichen von Angebot und Nachfrage sowie von Risiko- und Verfügbarkeitsprämien bestimmt wird, können Anomalien auftreten, die dazu führen, dass die Terminstrukturkurve invertiert verläuft.

Kommt es beispielsweise zu Ernteausfällen, wird kurzfristig ein Nachfrageüberhang am Markt für das betroffene Agrarprodukt anzutreffen sein. In der Folge würden die Marktpreise des Agrarprodukts stark ansteigen und gleichermaßen die Preise der darauf basierenden Futures-Kontrakte. Die Preise der Futures-Kontrakte mit kurzer Laufzeit wären damit höher als mit langer Laufzeit. In diesem Fall wäre die Terminstrukturkurve invertiert und würde mit zunehmender Laufzeit abfallen.

Grundformen der Terminstrukturkurve

Bei der Betrachtung der Terminstrukturkurve lassen sich drei Grundformen identifizieren. Die Begriffe Contango und Backwardation werden dabei verwendet, um die Struktur der Terminstrukturkurve zu definieren.

Im Wesentlichen wird mit diesen Begriffen die Beziehung der Terminkurse zum Kassakurs beschrieben. In der Praxis sowie in der Fachliteratur werden oft die englischen Begriffe Forward Rate und Spot Rate  oder Spot Price anstelle von Terminkurs und Kassakurs verwendet, weshalb diese im weiteren Verlauf Anwendung finden.

Contango („Normalform“)

Contango bezeichnet eine Situation, in der die Forward Rate über der Spot Rate liegt. Es wird also erwartet, dass der Preis eines Futures-Kontrakts mit längerer Laufzeit höher ist als der aktuelle Marktkurs bzw. der Preis der Futures-Kontrakte mit kürzerer Laufzeit. Bei Contango spricht man von der Normalform einer Terminstrukturkurve, die idealtypisch asymptotisch ansteigt.

Angenommen ein Futures-Kontrakt auf einen beliebigen Basiswert befindet sich in Contango. In diesem Fall würde der Preis für eine zukünftige Lieferung des Basiswerts, beispielsweise eines Rohstoffs oder Index, höher notiert, als die Spot Rate.

Somit tritt eine Contango-Situation dann auf, wenn aufgrund von verschiedenen Einflussfaktoren für die Zukunft steigende Preise im Basiswert erwartet werden. In der Folge steigt die Preiskurve des entsprechenden Futures-Kontrakts in Abhängigkeit zur Laufzeit an.

Backwardation („invertierte Form“)

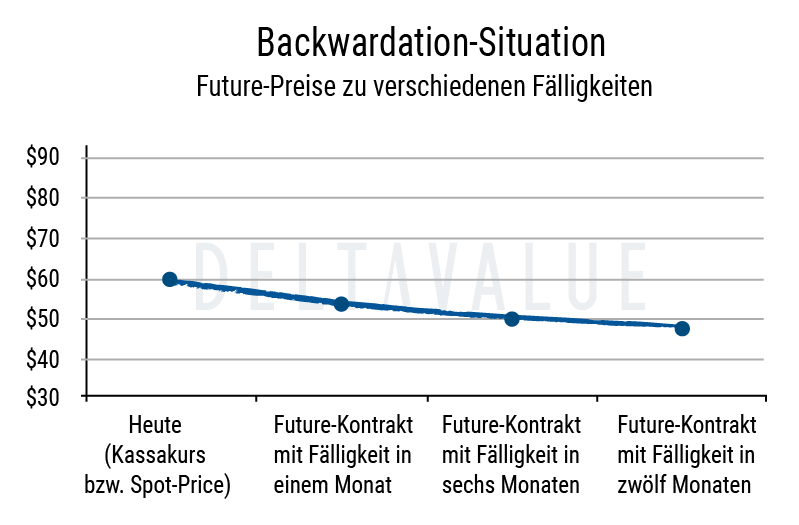
Backwardation bezeichnet eine Situation, in der die Forward Rate unter der Spot Rate liegt. Es wird also erwartet, dass der Preis eines Futures-Kontrakts mit längerer Laufzeit niedriger ist als der aktuelle Marktkurs bzw. der Preis der Futures-Kontrakte mit kürzerer Laufzeit. Bei Backwardation spricht man von der invertierten Form einer Terminstrukturkurve, die idealtypisch asymptotisch abfällt.

Angenommen ein Futures-Kontrakt auf einen beliebigen Basiswert befindet sich in Backwardation. In diesem Fall würde der Preis für eine zukünftige Lieferung des Basiswerts, beispielsweise eines Rohstoffs oder Index, niedriger notiert, als die Spot rate.

Somit tritt eine Backwardation-Situation dann auf, wenn für die Zukunft aufgrund von verschiedenen Einflussfaktoren niedrigere Preise im Basiswert erwartet werden. In der Folge sinkt die Preiskurve des entsprechenden Futures-Kontrakts in Abhängigkeit zur Laufzeit.

Flache Terminstrukturkurve

Eine flache Terminstrukturkurve bezeichnet eine Situation, in der die Preise der Futures-Kontrakte über alle Laufzeiten hinweg ähnliche Preise aufweisen. Die Forward Rate und die Spot Rate notieren in diesem Fall auf dem gleichen Preisniveau. Bei einer flachen Terminstrukturkurve ist es in der Regel schwer zu antizipieren, ob sie im weiteren Verlauf die Normalform (Contango) oder die invertierte Form (Backwardation) annimmt.

Diverse Zwischenformen

Neben den drei idealtypischen Grundformen, die eine Terminstrukturkurve annehmen kann, bestehen diverse Zwischenformen.

Bei Terminstrukturkurven kann sich beispielsweise ein Buckel in der Mitte ausbilden, wenn die Preise der Futures-Kontrakte mit kurzer und langer Laufzeit auf demselben Niveau liegen und gleichzeitig die Preise der Futures-Kontrakte mit mittlerer Laufzeit höhere Werte aufweisen.

Außerdem gibt es Situationen, in denen Terminstrukturkurven zu Beginn steigen, um schließlich wieder abzufallen. Dies ist der Fall, wenn die Preise der Futures-Kontrakte mit mittlerer Laufzeit über den Preisen der Futures-Kontrakte mit kurzer Laufzeit liegen, aber gleichzeitig die Preise der Futures-Kontrakte mit langer Laufzeit unter den Preisen der Futures-Kontrakte mit mittlerer und kurzer Laufzeit.

Ein verbreitetes Beispiel für Terminstrukturkurven, die sowohl steigende als auch fallende Terminkurse zeigen, sind saisonale Rohstoffe wie Weizen, Mais oder Mastrind. Je nach Saison resultieren Anfrage- und Nachfragebedingt entsprechende Preisschwankungen, die im Markt jedoch vorab bekannt sind und entsprechend auch in den Futures eingepreist werden. Üblicherweise werden dann bei der Analyse der Terminstruktur Future-Kontrakte mit gleichem Monatsverfall verglichen.

Terminstrukturkurve bei Rohstoffen

Die Terminstrukturkurve stellt insbesondere bei Rohstoffen ein elementar wichtiges Analyseinstrument dar. Dies ist dem Fakt geschuldet, dass es sich bei Rohstoffmärkten um Terminmärkte handelt.

Rohstoffe werden also mit Terminkontrakten wie Futures abgewickelt. Für jeden handelbaren Rohstoff gibt es mehrere Futures mit unterschiedlichen Fälligkeiten. Wie viele Fälligkeiten es gibt, hängt von dem jeweiligen Rohstoff ab. Jeder Futures repräsentiert also einen Liefertermin. Die einzelnen Preise der Futures ergeben letztlich die Terminstrukturkurve.

Beispiel

Als Anleger ist es wichtig zu verstehen, dass es nicht den einen Rohstoffpreis gibt, sondern der Futures-Preis für jede Fälligkeit separat ermittelt wird. In einer Contango-Situation, der Normalform der Terminstrukturkurve, notiert beispielsweise der WTI Rohöl Future mit Fälligkeit im Juni niedriger als der WTI Rohöl Future mit Fälligkeit im Oktober.

Es gibt also nicht nur einen Ölpreis, sondern eine ganze Reihe an Ölpreisen. Wenn in Finanzmedien vom Ölpreis die Rede ist, dann bezieht sich der dort genannte Wert auf den Spot Price.

Bedeutung

Das Verständnis der Preisbildung ist auch für die Anleger bedeutend, die keine Futures, sondern Hebelzertifikate handeln. Diese Hebelzertifikate beziehen sich immer auf einen Futures mit entsprechender Fälligkeit, also beispielsweise auf den WTI Rohöl Future mit Fälligkeit im Juni und eben nicht auf den Spot Price.

Oft kommt es daher in der Praxis vor, dass sich Anleger über die Preisentwicklung ihres Hebelzertifikates wundern, wenn bspw. der Spot Price im Wert steigt, aber ihr Hebelzertifikat an Wert verliert. Das hängt damit zusammen, dass sich der Wert des zugrundeliegenden Öl-Futures zuungunsten des Anlegers verändert hat.

Warum steigen die Preise von Rohstoff-Futures mit zunehmender Laufzeit?

Anders als bei Aktienindizes, handelt es sich bei Rohstoffen um physische Waren, die gelagert werden müssen. Dies verursacht unter anderem Finanzierungs- und Lagerkosten, die in der Fachsprache Cost of Carry genannt werden und wesentlich dazu beitragen, dass Futures-Preise im Normalfall höher notieren, je weiter der Liefertermin in der Zukunft liegt.

Weitere Kostenfaktoren können unter anderem Transport, Instandhaltung, Versicherungskosten, Transaktionskosten, Zinsen für entgangene Gewinne und sonstige Opportunitätskosten sein. All diese Kostenfaktoren, die ab der Produktion bis zur Lieferung anfallen, werden auf den Spot Price aufgeschlagen und im Futures-Preis einkalkuliert.

Sondersituation Backwardation bei Rohstoff-Futures

Bei Rohstoffen kann es aus verschiedenen Gründen zu einer Backwardation-Situation kommen. Disruptive Ereignisse können sich auf Angebot und Nachfrage auswirken. Solche Ereignisse können bspw. Ernteausfälle oder politische Konflikte darstellen. Diese können am Markt zu extremen Angebots- und Nachfrageüberhängen führen.

In der Folge steigen der Spot Price sowie die Futures-Preise mit nahen Lieferterminen signifikant an, weil es insbesondere für Unternehmen einen Vorteil sein könnte, das physische Material zu besitzen, um bspw. die Produktion aufrechtzuerhalten.

Dieser Effekt ist unter dem Namen Verfügbarkeitsprämie bekannt und ist eine implizite Rendite auf den Lagerbestand. Die Verfügbarkeitsprämie steht im entgegengesetzten Verhältnis zu den Lagerbeständen. Das bedeutet: hohe Lagerbestände führen zu einer geringen Verfügbarkeitsprämie, während niedrige Lagerbestände für eine hohe Verfügbarkeitsprämie sorgen.

Terminstrukturkurve beim VIX

Die verschiedenen Futures-Kontrakte auf den Cboe Volatility Index (VIX), werden ebenfalls in einer Terminstrukturkurve in Abhängigkeit zu ihrer Laufzeit abgebildet.

Allgemeinen gilt der VIX als Indikator für Marktrisiken und die Stimmung der Marktteilnehmer, da er die Markterwartungen hinsichtlich der Schwankungsintensität wiedergibt. Die Terminstrukturkurve des VIX zeigt demnach ein Stimmungsbild des Marktes in Form der eingepreisten Volatilitäten.

Wie bei den Terminstrukturkurven von Rohstoffen stellt die Contango-Situation auch bei der Terminstrukturkurve des VIX die Normalform dar. Das heißt, je länger die Laufzeit, umso höher der Preis der jeweiligen Futures-Kontrakte.

Da der VIX die Volatilität abbildet, kann man auch sagen, je länger die Laufzeit, umso höher die Erwartungen hinsichtlich der Volatilität. Wie bei allen Futures gilt auch hier, dass die Futures-Preise bei Annäherung an die Fälligkeit in Richtung des Spot Price, also dem VIX-Index selbst laufen.

Sondersituation Backwardation bei VIX-Futures

Eine Backwardation-Situation tritt beim VIX dann auf, wenn kurzfristig eine deutlich höhere Volatilität erwartet wird als mittel- bis langfristig, was für eine gewisse Unsicherheit im Markt spricht. Wichtig ist dabei, dass eine Backwardation-Situation nicht zwangsläufig eine Korrektur zur Folge hat.

Die Unsicherheit am Markt kann sich auch in volatilen Seitwärtsphasen bemerkbar machen, die ebenfalls kurzfristig für eine höhere Volatilität sorgen können. Jedoch gibt es am Markt keine Korrektur ohne Backwardation-Situation in der VIX-Terminstrukturkurve.

Theorien hinter der Terminstrukturkurve

Verschiedene Theorien versuchen zu erklären, warum die Normalform der Terminstrukturkurve aufwärtsgerichtet sein muss. Die zwei gängigsten Erklärungen beziehen sich auf den risikofreien Zinssatz und die Risikoprämie.

Risikofreier Zinssatz

Die erste Erklärung geht davon aus, dass die Marktteilnehmer grundsätzlich einen Anstieg des risikofreien Zinssatzes erwarten. Wenn ein Anleger also jetzt bereit ist sein Geld zu investieren und damit zu binden, dann muss dieser Anleger nach der Arbitragepreistheorie für den erwarteten Zinsanstieg entschädigt werden. Entsprechend weisen Anlagen mit längerer Laufzeit höhere Zinssätze auf als mit kurzer Laufzeit.

Risikoprämie

Eine andere Erklärung für die aufwärtsgerichtete Normalform der Terminstrukturkurve ist, dass längere Laufzeiten für den Anleger mit größeren Risiken verbunden sind. Je länger die Laufzeit, desto größer die Wahrscheinlichkeit, dass sich disruptive Ereignisse negativ auf die Investition auswirken. Deshalb wird eine Risikoprämie gefordert.

Dieser Mechanismus ist auch als Liquiditätsspreadrisiko bekannt. Trotz sinkender risikofreier Zinssätze, kann in Erwartung hoher Volatilität die Renditen steigen, aufgrund einer steigenden Risikoprämie.