CAPM (Capital Asset Pricing Model) – Definition & Berechnung

Das Capital Asset Pricing Model (CAPM), auf Deutsch „Preismodell für Kapitalgüter“, ist ein theoretisches Kapitalmarktmodell zur Analyse von Risiko und Rendite von Wertpapieren. Ziel des Modells ist es, erwartete Renditen basierend auf dem eingegangenen Risiko zu bestimmen. Das CAPM-Modell dient zudem als Grundlage für weitere Bewertungsmodelle wie die Discounted-Cashflow-Methode.

CAPM – Definition

Das Capital Asset Pricing Model (CAPM) beschreibt die Beziehung zwischen dem systematischen Risiko und der erwarteten Rendite eines Wertpapiers oder eines Portfolios am Kapitalmarkt. Das Ergebnis liefert eine Antwort auf die Frage, wie hoch die Renditeerwartung der Shareholder für eine bestimmte Aktie sein sollte.

Als Modell zur Berechnung der erwarteten Rendite und der Eigenkapitalkosten stützt sich das CAPM auf die Portfoliotheorie. Diese besagt, dass das Risiko durch Diversifikation – also eine möglichst geringe Korrelation der einzelnen Werte im Portfolio – reduziert werden kann.

Das CAPM erweitert die Portfoliotheorie, indem es nicht nur ein optimales Portfolio definiert, sondern auch das Risiko identifiziert, das durch Diversifikation nicht eliminiert werden kann (systematisches Risiko).

Berechnung des CAPM

Das CAPM geht bei der Berechnung von einem risikolosen Zinssatz und einer Risikoprämie aus. Diese Risikoprämie setzt sich zusammen aus dem individuellen Betafaktor (Risikofaktor) eines Unternehmens multipliziert mit der durchschnittlichen Renditedifferenz der Anlageklasse (z.B. Aktien vs. Staatsanleihen).

Die CAPM-Formel lautet wie folgt:

Bestandteile des Modells sind:

• Risikofreier Zins:
  Dies ist die Rendite einer sicheren Anlage, zum Beispiel von Staatsanleihen. Er dient als Basisrendite, die ein Anleger ohne Risiko erhalten würde.
• Beta (β):
  Der Betafaktor misst die Volatilität bzw. das Risiko einer Aktie im Vergleich zum Gesamtmarkt.
  • Ein Beta = 1 bedeutet, dass die Aktie genauso volatil ist wie der Markt.
  • Ein Beta > 1 zeigt ein höheres Risiko (größere Schwankungen als der Markt).
  • Ein Beta < 1 weist auf ein geringeres Risiko hin.
• Marktrisikoprämie:
  Dies ist der zusätzliche Ertrag, den Anleger erwarten, wenn sie in risikoreiche Anlagen (z.B. Aktien) statt in risikofreie Anlagen investieren. Sie berechnet sich als Differenz zwischen der erwarteten Marktrendite und dem risikofreien Zins.

Beispiel für die Anwendung der CAPM-Formel

Ein Investor analysiert ein Unternehmen mit einem Aktienkurs von 100 Euro. Die Rendite von Staatsanleihen beträgt 1 %. Das Unternehmen hat ein Beta von 1,5 und ist damit als riskanter beziehungsweise volatiler als der Markt einzustufen. Der Investor erwartet eine Marktrendite in Höhe von 8 %.

Darauf ergibt sich folgende CAPM-Berechnung:

Der Zinssatz von 11,5 % kann im Folgenden als Diskontierungsfaktor für die zukünftigen Cashflows verwendet werden:

• Erzielt ein Unternehmen ein jährliches Wachstum von 11,5 %, so würde die Diskontierung genau den heutigen Aktienkurs ergeben.
• Sind die Ertragsaussichten höher als die Erwartungen des Investors, kann die Aktie als unterbewertet angesehen werden bzw. stellt eine attraktive Investitionsmöglichkeit dar.

Was ist die Effizienzkurve?

Die Effizienzkurve (auch effiziente Grenze genannt) zeigt alle Kombinationen von Portfolios, die für ein gegebenes Risiko die höchste erwartete Rendite liefern. Die Kapitalmarktlinie (CML) stellt alle möglichen Kombinationen aus dem risikofreien Zinssatz und dem optimalen Portfolio dar. Diese Portfolios bieten die bestmögliche Rendite pro Risikoeinheit und gelten als über der Effizienzkurve liegend, sofern Fremdfinanzierung genutzt wird.

Der Schnittpunkt zwischen der Kapitalmarktlinie und der Effizienzkurve markiert das optimale Portfolio. Es stellt das Portfolio dar, das das beste Verhältnis von Risiko zu erwarteter Rendite aufweist. Von diesem Punkt ausgehend lässt sich durch Mischung mit einer risikofreien Anlage jedes gewünschte Risiko-Rendite-Profil entlang der Kapitalmarktlinie abbilden.

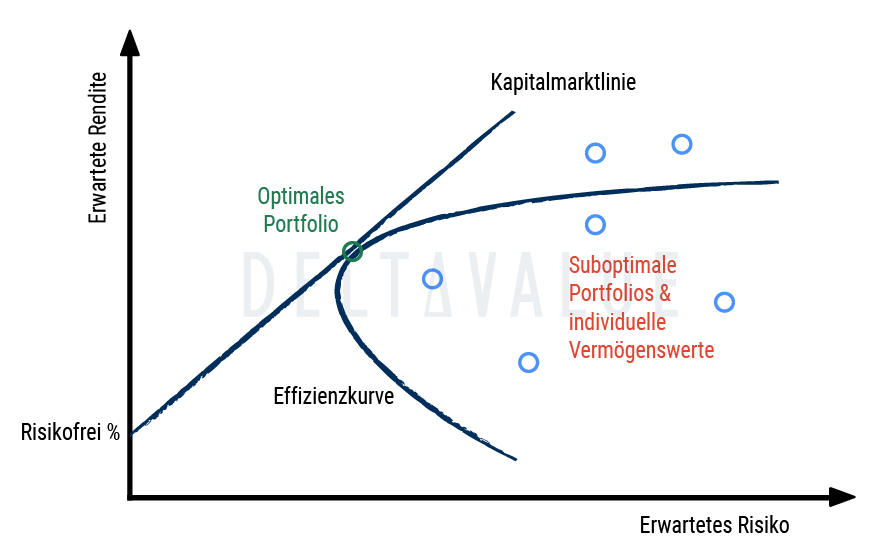
• Die y-Achse der Grafik zeigt die erwartete Rendite, wobei der risikofreie Zinssatz den Startpunkt der Kapitalmarktlinie bildet. Dieser Zinssatz kann ohne Eingehen eines Risikos erzielt werden.
• Die auf der rechten Seite eingezeichneten Einzelpunkte symbolisieren suboptimale Portfolios oder einzelne Vermögenswerte, da sie bei gleichem Risiko eine geringere Rendite bieten würden.

Beispiel für eine optimale Portfolioallokation

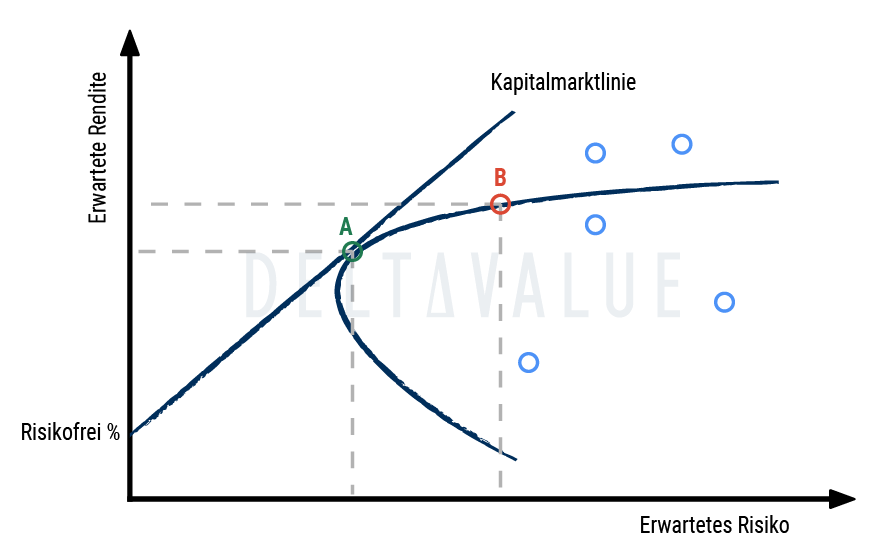
Die folgende Abbildung zeigt zwei Portfolios (A und B) auf der Effizienzkurve. Beide gelten als effizient, weil sie im Verhältnis zum eingegangenen Risiko eine bestmögliche erwartete Rendite liefern.

• Portfolio A liegt genau am Schnittpunkt zwischen Effizienzkurve und Kapitalmarktlinie. Es stellt das optimale Portfolio im Sinne des CAPM dar. Dieses Portfolio erzielt beispielsweise eine erwartete Rendite von 8 % bei einer Standardabweichung von 10 %.
• Portfolio B befindet sich ebenfalls auf der Effizienzkurve und bietet eine etwas höhere Rendite, jedoch zu einem deutlich höheren Risiko. Die zusätzliche Rendite erfolgt nicht proportional zur Risikozunahme, was die abnehmende Effizienz bei wachsendem Risiko verdeutlicht.

Theoretisch liefert jedes Portfolio auf der Effizienzkurve die höchste Rendite für das jeweilige Risiko. Diese Kurve basiert auf denselben Annahmen wie das Capital Asset Pricing Model (CAPM) – etwa vollständige Information, rationales Verhalten und Marktliquidität – und ist somit ein theoretisches Konstrukt.

In der Praxis sind Renditeprognosen unsicher. Daher kann die genaue Lage und Form der Effizienzkurve lediglich geschätzt werden. Trotzdem dient sie als wichtiges Instrument zur Orientierung bei der Portfoliozusammenstellung und Risikosteuerung.

CAPM  – Nachteile

Ein zentraler Kritikpunkt des CAPM ist die starke Vereinfachung der Realität. Das Modell basiert auf der Annahme eines vollkommenen Kapitalmarkts, der in der Praxis nicht existiert. Die Behavioral Finance hat zudem nachgewiesen, dass Kapitalmärkte ineffizient sind: Informationsasymmetrien bestehen, und viele Investoren handeln irrational oder nur eingeschränkt rational – oft entgegen dem Ziel der Renditemaximierung.

Ein weiterer Schwachpunkt ist die Verwendung des Betafaktors zur Risikomessung. Beta beruht auf der Volatilität, die vergangenheitsorientiert berechnet wird und somit keine verlässliche Aussage über aktuelle oder zukünftige Risiken erlaubt. Zudem erfasst Beta nur Kursbewegungen, nicht jedoch deren Richtung oder Ursache.

Das CAPM nimmt außerdem einen konstanten risikolosen Zinssatz über den gesamten Bewertungszeitraum an – eine Annahme, die in der Realität selten zutrifft. Veränderungen des Zinssatzes können dazu führen, dass Anlagen fälschlicherweise über- oder unterbewertet erscheinen.

Auch die Marktrisikoprämie im CAPM steht in der Kritik. Sie wird häufig aus nationalen oder internationalen Indizes abgeleitet, die den Gesamtmarkt nur unvollständig abbilden. Da es keine realistische Alternative zur direkten Investition in den gesamten Markt gibt, bleibt die Marktrisikoprämie eine ungenaue Schätzung.

Abschließend setzt das CAPM voraus, dass zukünftige Renditen und Cashflows zuverlässig prognostizierbar sind. Wäre dies tatsächlich möglich, wäre das CAPM als Modell überflüssig.

CAPM – Vorteile

Ein wesentlicher Vorteil des CAPM liegt in seiner Einfachheit und schnellen Anwendbarkeit, auch für weniger erfahrene Investoren. Mit wenigen Annahmen lässt sich die erforderliche Rendite eines Wertpapiers berechnen und mit den eigenen Erwartungen abgleichen. Dies ermöglicht es, unterschiedliche Prognosen miteinander zu vergleichen und zu validieren, wodurch das CAPM als Diskussionsgrundlage für fundierte Investitionsentscheidungen dient.

Darüber hinaus eignet sich das CAPM zur Überprüfung bestehender Portfolios. Angenommen, ein Portfolio erzielt die gleiche Rendite wie ein breit diversifiziertes ETF, weist jedoch eine höhere Volatilität auf (z. B. 12 % statt 8 %). In diesem Fall bietet das ETF die effizientere Lösung, da die gleiche Rendite bei geringerem Risiko erzielt wird. Mithilfe des CAPM kann der Anleger somit sein Portfolio anpassen und das Risiko-Rendite-Verhältnis optimieren.

Exkurs: Portfoliotheorie

Der amerikanische Ökonom Harry M. Markowitz legte in den 1950er-Jahren mit der Entwicklung der Portfoliotheorie (auch Portefeuilletheorie) den Grundstein für die moderne Finanzmarktforschung. Seine Arbeit bildet nicht nur die theoretische Basis für das Capital Asset Pricing Model (CAPM), sondern auch für andere finanzwirtschaftliche Modelle wie die Arbitragepreistheorie (APT).

Markowitz war der erste Wissenschaftler, der den Zusammenhang zwischen Diversifikation, Risiko und Rendite eines Portfolios mathematisch beschrieb. Er zeigte, dass die Investition in nur ein Wertpapier ein weitaus höheres Risiko birgt als die Streuung des Kapitals über mehrere Anlagewerte. Sein Fokus lag darauf, ein optimales Aktienportfolio zu entwickeln, das durch die geschickte Kombination von Wertpapieren das Gesamtrisiko bei gegebener erwarteter Rendite minimiert.

Systematisches vs. unsystematisches Risiko

Kernbegriffe der Portfoliotheorie sind das systematische Risiko, das durch Marktschwankungen bedingt und nicht eliminierbar ist, sowie das unsystematische Risiko, das durch Diversifikation verringert werden kann.

Korrelation von Aktien und ihrer Kursentwicklung

In der Portfoliotheorie spielt ebenfalls die Korrelation von Aktien und deren Kursentwicklung eine entscheidende Rolle. Der Begriff Korrelation beschreibt, wie stark die Kursentwicklung von zwei Aktien übereinstimmt.

• Bei einem Wert von 1 entwickeln sich beide Werte identisch. Es liegt eine perfekt positive Korrelation vor.
• Ein Wert von -1 entsteht dagegen, wenn sich die Kurse der Aktien genau entgegengesetzt bewegen.
• Bei einer Korrelation von 0 findet die Entwicklung der beiden Werte unabhängig voneinander statt.

Aktien mit niedriger oder negativer Korrelation senken folglich nach der Annahme von Markowitz das Risiko eines Aktienportfolios. Für das CAPM ist diese Erkenntnis wichtig, da es systematisches Risiko als das einzige relevante Risiko für Anleger betrachtet. Ein Anleger, der optimal diversifiziert ist, muss sich nur noch mit dem systematischen Risiko auseinandersetzen.