Kurtosis – Definition & Bedeutung

Kurtosis – Definition

Die Kurtosis (Wölbung) ist das vierte standardisierte zentrale Moment einer Verteilung. Formal gilt für eine Zufallsvariable X mit Erwartungswert μ und Standardabweichung σ:

• Kurtosis (Pearson-Kurtosis):
  \beta_2=\mathbb{E}\left[\left(\frac{X-\mu}{\sigma}\right)^4\right]=\frac{\mu^4}{\sigma^4}
• Exzesskurtosis:
  \gamma_2=\beta_2-3

Die Normalverteilung hat Kurtosis = 3 und damit Exzesskurtosis = 0. In vielen Anwendungen (u. a. in der Finanzpraxis) wird daher bevorzugt die Exzesskurtosis berichtet, weil sie direkt zeigt, ob die Verteilung im Vergleich zur Normalverteilung dickere oder dünnere Tails besitzt.

Kurtosis und Peakedness

Die Kurtosis wird im Alltag häufig mit der „Spitzenhaftigkeit“ (engl. peakedness) einer Verteilung gleichgesetzt. Tatsächlich ist diese Gleichsetzung jedoch nur eingeschränkt sinnvoll: Kurtosis (bzw. Exzesskurtosis) beschreibt vor allem, wie stark extreme Werte im Vergleich zur Normalverteilung zu erwarten sind.

Eine Verteilung kann beispielsweise einen sehr ausgeprägten Gipfel haben, ohne besonders dicke Tails zu besitzen – und umgekehrt können dicke Tails auftreten, ohne dass der Gipfel „spitzer“ wirkt. Deshalb kann es sinnvoller sein, Kurtosis vor allem als Maß für die Tail-Heaviness bzw. Ausreißer-Neigung zu verstehen.

Skewness

Skewness (deutsch: „Schiefe“) misst, wie (a)symmetrisch eine Verteilung ist – also ob der linke oder rechte Rand (Tail) stärker ausgeprägt ist und die Verteilung dadurch zur einen oder anderen Seite „schief“ wird.

Während die Schiefe beschreibt, auf welcher Seite Extremwerte eher auftreten (Asymmetrie), beschreibt die (Exzess-)Kurtosis, wie stark Extremwerte insgesamt (auf beiden Seiten) im Vergleich zur Normalverteilung ausgeprägt sind.

Kategorien der Kurtosis

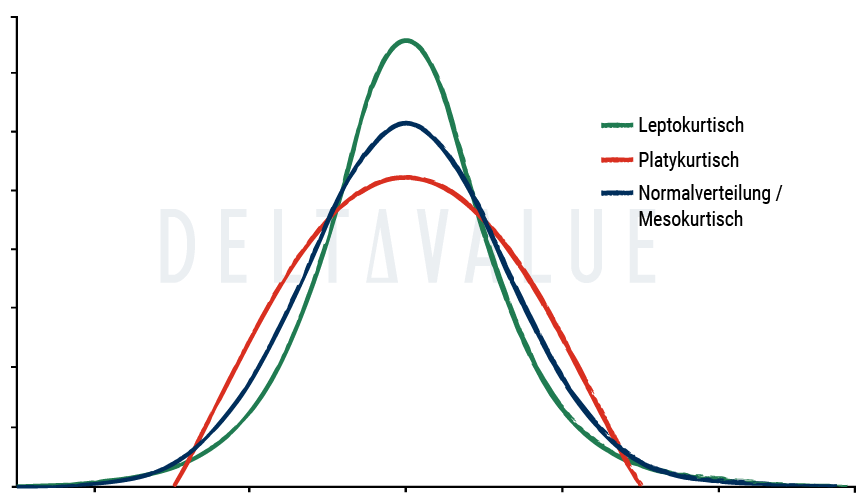
Es gibt drei gängige Kategorien, um Kurtosis im Vergleich zur Normalverteilung einzuordnen. Dabei ist wichtig, ob du über Kurtosis (Referenzwert der Normalverteilung: 3) oder über Exzesskurtosis (Referenzwert: 0) sprichst.

• Leptokurtische Verteilung: positive Exzesskurtosis (γ₂ > 0). Typisch sind dickere Tails („Fat Tails“), d. h. extreme Werte treten häufiger auf als bei der Normalverteilung. Beispiel: Laplace-Verteilung, auch t-Verteilungen mit kleinen Freiheitsgraden sind klassisch leptokurtisch (bei genügend Freiheitsgraden ist die Kurtosis endlich).
• Platykurtische Verteilung: negative Exzesskurtosis (γ₂ < 0). Typisch sind dünnere Tails, d. h. extreme Werte sind seltener als bei der Normalverteilung. Beispiel: Gleichverteilung (Uniformverteilung).
• Mesokurtische Verteilung: Exzesskurtosis nahe 0 (γ₂ ≈ 0). Die Tail-Ausprägung ist ähnlich wie bei der Normalverteilung. Beispiel: Normalverteilung.

Mesokurtische Verteilung

Die mesokurtische Verteilung hat eine (Exzess-)Kurtosis, die der Normalverteilung ähnlich ist (γ₂ ≈ 0). Das bedeutet: Das Gewicht in den Randbereichen ist in etwa so ausgeprägt wie bei einer Normalverteilung.

Leptokurtische Verteilung

Die zweite Kategorie ist eine leptokurtische Verteilung. Die Vorsilbe „lepto-“ bedeutet „dünn/schlank“ und wird historisch mit einer „spitzen“ Erscheinung in Verbindung gebracht. Statistisch entscheidend ist aber: Leptokurtische Verteilungen haben positive Exzesskurtosis und damit dickere Tails als die Normalverteilung.

Das bedeutet:

• Im Vergleich zur Normalverteilung liegt mehr Wahrscheinlichkeit in den Tails.
• Dadurch treten sehr große Abweichungen (z. B. Ereignisse jenseits von ±3σ) häufiger auf.

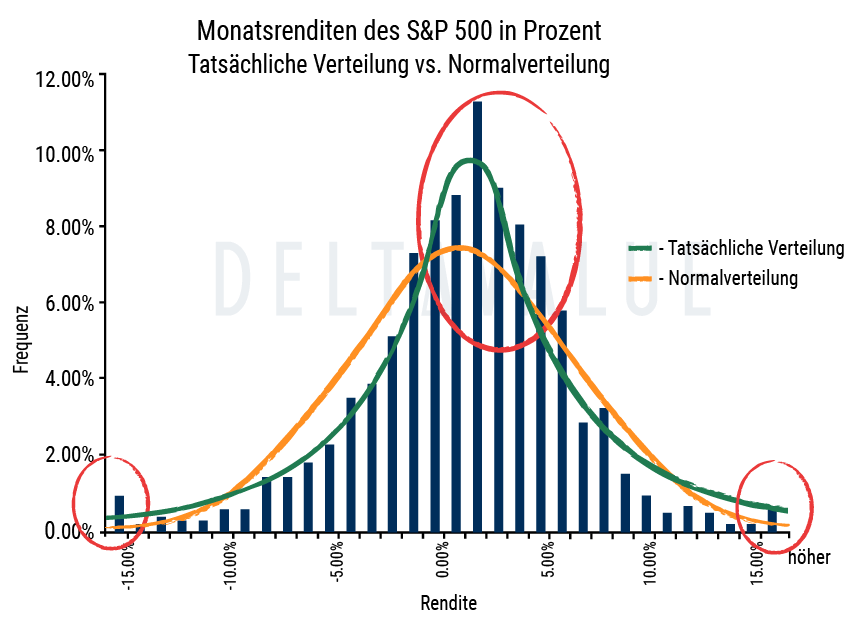
Aktien- und Indexrenditen (z. B. S&P 500) sind häufig leptokurtisch, weisen also positive Exzesskurtosis auf: Es treten mehr/extremere Ausschläge auf, als es eine Normalverteilung erwarten ließe.

Platykurtische Verteilung

Der letzte Verteilungstyp ist eine platykurtische Verteilung. Die Vorsilbe „platy-“ bedeutet „breit“. Platykurtische Verteilungen haben negative Exzesskurtosis, also dünnere Tails als die Normalverteilung. Extreme Ausreißer sind im Vergleich zur Normalverteilung tendenziell seltener.

Bedeutung der Kurtosis für Anleger

Für Anleger bedeutet eine leptokurtische Renditeverteilung, dass extreme Renditen (positiv oder negativ) im Vergleich zur Normalverteilung häufiger auftreten können. Dieses Phänomen wird häufig als Tail-Risiko bzw. „Kurtosis-Risiko“ bezeichnet. Leptokurtisch heißt aber nicht „mehr Crashes als Rallyes“ – das wäre eher Skewness.

Eine platykurtische Verteilung deutet dagegen darauf hin, dass extreme Ausreißer im Vergleich zur Normalverteilung tendenziell seltener sind. Das garantiert jedoch keine „Vorhersehbarkeit“, sondern ist lediglich ein statistischer Hinweis auf die Tail-Struktur.